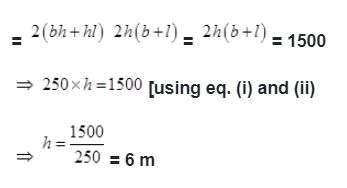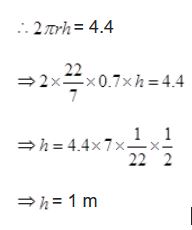NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas and Volumes
These solutions contain critical questions and exercises intrinsic to the chapter, including definitions, formulas, and calculations. Solutions are clearly and concisely presented so that students can understand and learn core concepts easily.
Access Answers to NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas and Volumes
Students can access the NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas and Volumes. Curated by experts according to the CBSE syllabus for 2023–2024, these step-by-step solutions make Maths much easier to understand and learn for the students. These solutions can be used in practice by students to attain skills in solving problems, reinforce important learning objectives, and be well-prepared for tests.
Exercise 11.1
The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of Rs. 7.50 per m2.
Given: Length (l)= 5 m, Breadth (b)= 4 m and Height (h)= 3 m
= 2 x 3 (4 + 5)
= 2 x 9 x 3 = 54 m2
Area of ceiling = = 5 x 4 = 20 m2
Now Cost of white washing for 1 m2 = Rs. 7.50
Cost of white washing for 74 m2 = 74 x 7.50 = Rs. 555
A plastic box 1.5 m long, 1.25 m wide and 65 cm deep is to be made. It is to be open at the top. Ignoring the thickness of the plastic sheet, determine :
(i) The area of the sheet required for making the box.
(ii) The cost of sheet for it, if a sheet measuring 1m2 cost Rs.20.
Solution:
(i) Given: Length (l)= 1.5 m, Breadth (b)= 1.25 m and Depth (h)
= 65 cm = 0.65 m
Area of the sheet required for making the box open at the top =2(bh+hl)+lb
= 2(1.25*0.65+*1.5)+1.5*1.25
= 2(0.8125+0.975)+1.875
= 2*1.7875+1.875
= 3.575 + 1.875 = 5.45 m2
(ii) Since, Cost of 1 m2 sheet = Rs. 20
Cost of 5.45 m2 sheet = 20 x 5.45 = Rs. 109
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of Rs. 10 per m2 is Rs. 15000, find the height of the hall.
Given: Perimeter of rectangular wall
= 2(l+b)= 250 m ……….(i)
Now Area of the four walls of the room
=total cost to paint wallsof the room/cost paint to 1 m2 of the walls
=1500/10 = 1500 m2 ……….(ii)
Area of the four walls = Lateral surface area
Hence required height of the hall is 6 m.
The paint in a certain container is sufficient to paint an area equal to 9.375 m2. How many bricks of dimensions 22.5 cm x 10 cm x 7.5 cm can be painted out of this container?
Given: Length of the brick (l)
= 22.5 cm, Breadth (b)
= 10 cm and Height (h)= 7.5 m
= 2(lb+bh+hl)
= 2 (22.5 x 10 + 10 x 7.5 + 7.5 x 22.5)
= 2 (225 + 75 + 468.75)
= 937.5 cm2
= 0.09375 m2 [1 cm = 0.01 m]
Now No. of bricks to be painted
total area of to be painted/area of bricks=9.375/0.09375
= 100
Hence 100 bricks can be painted.
A cubical box has each edge 10 cm and a cuboidal box is 10 cm wide, 12.5 cm long and 8 cm high.
(i) Which box has the greater lateral surface area and by how much?
(ii) Which box has the smaller total surface area and how much?
Solution:
(i) Lateral surface area of a cube = 4 (side)2 = 4 x (10)2 = 400 cm2
Lateral surface area of a cuboid = 2h(b+l)
= 2 x 8 (12.5 + 10) = 16 x 22.5 = 360 cm2
(ii) Total surface area of a cube = 6 (side)2
= 6 x (10)2 = 600 cm2
Total surface area of cuboid = 2h(lb+bh+hl)
= 2 (12.5 x 10 + 10 x 8 + 8 x 12.5)
= 2 (125 + 80 + 100)
= 2 x 305 = 610 cm2
A small indoor green house (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.
(i) What is the surface area of the glass?
(ii) How much of tape is needed for all the 12 edges?
(i) Given: Length of glass herbarium (l)= 30 cm,
Breadth (b)= 25 cm and Height (h)= 25 m
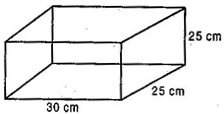
Total surface area of the glass
= 2(lb+bh+hl)
= 2 (30 x 25 + 25 x 25 + 25 x 30)
= 2 (750 + 625 + 750)
= 2 x 2125 = 4250 cm2
Hence 4250 cm2 of the glass is required to make a herbarium.
(ii) Tape is used at 12 edges.
= 2 (30 + 25 + 25) = 320 cm
Hence 320 cm of the tape if needed to fix 12 edges of herbarium.
Shanti Sweets Stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25 cm by 20 cm by 5 cm and the smaller of dimensions 15 cm by 12 cm by 5 cm. 5% of the total surface area is required extra, for all the overlaps. If the cost of the card board is Rs. 4 for 1000 cm2, find the cost of cardboard required for supplying 250 boxes of each kind.
Given: Length of bigger cardboard box (L) = 25 cm
Breadth (B) = 20 cm and Height (H) = 5cm
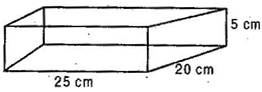
Total surface area of bigger cardboard box
= 2 (LB + BH + HL)
= 2 (25 x 20 + 20 x 5 + 5 x 25)
= 2 (500 + 100 + 125)
= 1450 cm2
5% extra surface of total surface area is required for all the overlaps.
Now, total surface area of bigger cardboard box with extra overlaps
= 1450 + 72.5 = 1522.5 cm2
= 250 x 1522.5 = 380625 cm2
Since, Cost of the cardboard for 1000 cm2 = Rs. 4
= Rs. 4/1000*38605= Rs. 1522.50
Now length of the smaller box (l)= 15 cm,
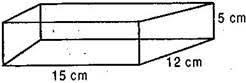
Breadth (b)= 12 cm and Height (h)= 5 cm
Total surface area of the smaller cardboard box
= 2(lb+bh+hl)
= 2 (15 x 12 + 12 x 5 + 5 x 15)
= 2 (180 + 60 +75) = 2 x 315 = 630 cm2
5% of extra surface of total surface area is required for all the overlaps.
Total surface area with extra overlaps = 630 + 31.5 = 661.5 cm2
Now Total surface area with extra overlaps of 250 such smaller boxes
= 661.5 x 250 = 165375 cm2
Cost of the cardboard for 1000 cm2 = Rs. 4
Cost of the cardboard for 1cm2 = Rs. 4/1000
Cost of the cardboard for 165375 cm2 = Rs. 4/1000*165375= Rs. 661.50
= Total cost of bigger boxes + Total cost of smaller boxes
= Rs. 1522.50 + Rs. 661.50
= Rs. 2184
Parveen wanted to make a temporary shelter for her car, by making a box-like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m with base simensions 4 m x 3 m?
Given: Length of base (l)= 4 m, Breadth (b)
= 3 m and Height (h)= 2.5 m
Tarpaulin required to make shelter
= Surface area of 4 walls + Area of roof
= 2h(l+b)+lb
= 2 (4 + 3) 2.5 + 4 x 3
= 35 + 12 = 47 m2
Hence 47 m2 of the tarpaulin is required to make the shelter for the car.
Exercise 11.2
A metal pipe is 77 cm long. The inner diameter of a cross section is 4 cm, the outer diameter being 4.4 cm. [See fig.]. Find its :
(i) Inner curved surface area
(ii) Outer curved surface area
(iii) Total surface area
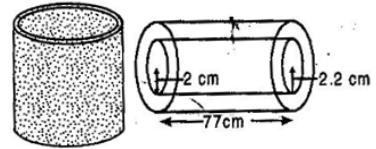
(i) Length of the pipe = 77 cm, Inner diameter of cross-section = 4 cm
Inner radius of cross-section = 2 cm
Inner curved surface area of pipe = 2πrh=2 * 22/7 * 2 * 77
= 2 x 22 x 2 x 11 = 968 cm2
(ii) Length of pipe = 77 cm, Outer diameter of pipe = 4.4 cm
Outer surface area of the pipe =2πrh
=2 * 22/7 * 2 * 77
= 44 x 2.2 x 11 = 1064.8 cm2
(iii) Now there are two circles of radii 2 cm and 2.2 cm at both the ends of the pipe.
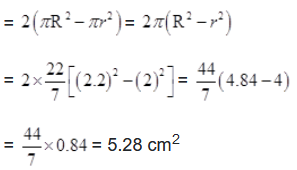
= 5.28 cm2
Total surface area of pipe
= Inner curved surface area + Outer curved surface area + Area of two edges
= 968 + 1064.8 + 5.28 = 2038.08 cm2
A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of white washing the curved surface of the pillar at the rate of Rs. 12.50 per m2.
Diameter of pillar = 50 cm
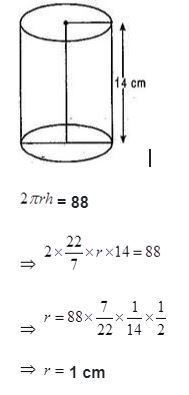
The curved surface area of a right circular cylinder of height 14 cm is 88 cm2. Find the diameter of the base of the cylinder.
Given: Height of cylinder (h)= 14 cm, Curved Surface Area = 88 cm2
Let radius of base of right circular cylinder = r cm
Diameter of the base of the cylinder = 2r= 2 x 1 = 2 c=>m
It is required to make a closed cylindrical tank of height 1 m and base diameter 140 cm from a metal sheet. How many square meters of the sheet are required for the same?
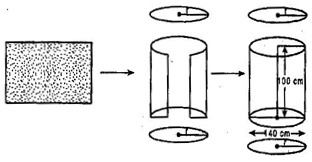
Given: Diameter = 140 cm
Hence 7.48 m2 metal sheet is required to make the close cylindrical tank.
The diameter of a roller is 84 cm and its length is 120 cm. It takes 500 complete revolutions to move once over to level a playground. Find the area of the playground in m2.
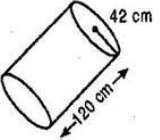
Radius of the roller = 42 cm
Length (Height) of the roller = 120 cm
Curved surface area of the roller = 2πrh
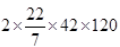
= 3.1680 m2
Now area leveled by roller in one revolution = 3.1680 m2
Area leveled by roller in 500 revolutions
= 3.1680 x 500 = 1584.0000 = 1584 m2
Diameter of roller = 84 cm
Curved surface area of a right circular cylinder is 4.4 m2. If the radius of the base of the cylinder is 0.7 m, find its height.
Curved surface area of the cylinder
= 4.4 m2, Radius of cylinder = 0.7 m
Let height of the cylinder = h
The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find :
(i) its inner curved surface area.
(ii) thecosr of plastering this curved surface at the rate of Rs. 40 per m2.
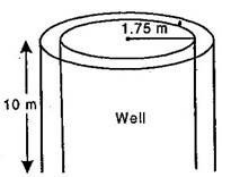
Inner diameter of circular well = 3.5 m
Inner radius of circular well
= 3.5/2= 1.75 m
And Depth of the well = 10 m
(i) the lateral or curved surface area of a petrol storage tank that is 4.2 m in diameter and 4.5 m high.
(ii) how much steel was actually used if 1/12 of the steel actually used was wasted in making the tank?
The length (height) of the cylindrical pipe = 28 m
Diameter = 5 cm
Curved surface area of the pipe =2πrh
(i) Diameter of cylindrical petrol tank = 4.2 m
= 4.2/2= 2.1 m
And Height of the tank = 4.5 m
In the adjoining figure, you see the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of 20 cm and height of 30 cm. A margin of 2.5 cm is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade. [See fig.]
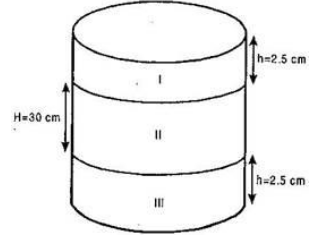
Height of each of the folding at the top and bottom (h)= 2.5 cm
Height of the frame (H) = 30 cm
Diameter = 20 cm
Now cloth required for covering the lampshade
= CSA of top part + CSA of middle part + CSA of bottom part
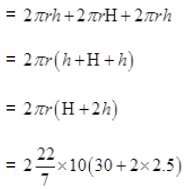
= 2200 cm2
he students of a Vidyalayawere asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?
Radius of a cylindrical pen holder (r)= 3 cm
Height of the cylindrical pen holder (h)
= 10.5 cm
Cardboard required for pen holder = CSA of pen holder + Area of circular base
Exercise 11.3
Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area and its total surface area.
Diameter = 10.5 cm
Slant height of cone (l)= 10 cm
Curved surface area of cone= πr(l + r)
= 
Total surface area of cone = πr(l + r)
=
= 
Find the total surface area of a cone, if its slant height is 21 cm and diameter of the base is 24 cm.
Slant height of cone (l)= 21 m
Diameter of cone = 24 m
Total surface area of cone = πr(l + r)
=
= 
Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find (i) radius of the base and (ii) total surface area of the cone.
(i) Slant height of cone (l)= 14 cm
Curved surface area of cone = 308 cm2
(ii) Total surface area of the cone
= Curved surface area + Area of circular base
= 462 cm2
A conical tent is 10 m high and the radius of its base is 24 m. Find:
(i) slant height of the tent.
(ii) cost of the canvas required to make the tent, if the cost of a m2 canvas is Rs. 70.
Height of the conical tent(
Radius of the conical tent (r)= 24 m
(i) Slant height of the tent
(ii) Canvas required to make the tent
= Curved surface area of the tent= πrl
= 
Cost of 1 m2 canvas = Rs. 70
Cost of 
= 70 x 
What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. ( Use π = 3.14)
Height of the conical tent (
Slant height of the tent
Area of tarpaulin = Curved surface area of tent = πrl= 3.14 x 6 x 10 = 188.4 m2
Width of tarpaulin = 3 m
Let Length of tarpaulin = L
Area of tarpaulin = Length x Breadth
= L x 3 = 3L
Now According to question,
3L = 188.4
The extra length of the material required for stitching margins and cutting is 20 cm = 0.2 m.
So the total length of tarpaulin bought is (62.8 + 0.2) m = 63 m
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of whitewashing its curved surface at the rate of Rs. 210 per 100 m2.
Slant height of conical tomb (l)
= 25 m, Diameter of tomb = 14 m
Radius of the tomb (r) = 14/2 = 7 m
Curved surface are of tomb = πrl
= 
Cost of white washing 100 m2
= Rs. 210
So, Cost of white washing 1 m2 =
So, Cost of white washing 550 m2
= 
A Joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
Radius of cap (r)= 7 cm,
Height of cap (
Slant height of the cone
= 25 cm
Area of sheet required to make a cap
= CSA of cone = πrl
= 
Area of sheet required to make 10 caps = 10 x 550 = 5500 cm2
A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is Rs. 12 per m2, what will be the cost of painting all these cones?
Diameter of cone = 40 cm
Radius of cone (r)=40/2 = 20 cm
= 20/100 m = 0.2 m
Height of cone (
Slant height of cone
= 
Curved surface area of cone =
= 3.14 x 0.2 x
= 0.64056 m2
Cost of painting 1 m2 of a cone
= Rs. 12
Cost of painting 0.64056 m2 of a cone
= 12 x 0.64056= Rs. 7.68672
Cost of painting of 50 such cones
= 50 x 7.68672 = Rs. 384.34 (approx.)
Exercise 11.4
The diameter of the moon is approximately one fourth the diameter of the earth. Find the ratio of their surface areas.
Let diameter of Earth =
=
Now, Diameter of Moon = 
Surface area of Moon = 4πr2
=
Now, Ratio =
=
Find the surface area of a sphere of radius:
(i) 10.5 cm
(ii) 5.6 cm
(iii) 14 cm
(i) Radius of sphere = 105 cm
Surface area of sphere = 4πr2
= 
(ii) Radius of sphere = 5.6 m
Surface area of sphere = 4πr2
= 
(iii) Radius of sphere = 14 cm
Surface area of sphere = 4πr2
= 
Find the surface area of a sphere of diameter:
(i) Diameter of sphere = 14 cm,
Therefore Radius of sphere = 14/2 = 7 cm
Surface area of sphere = 4πr2
= 
(ii) Diameter of sphere = 21 cm
Radius of sphere = 21/2 cm
Surface area of sphere = 4πr2
= 
(iii) Diameter of sphere = 3.5 cm
Radius of sphere = 3.5/2 = 1.75 cm
Surface area of sphere = 4πr2
= 
Find the total surface area of a hemisphere of radius 10 cm.
(Use π =3.14)
Radius of hemisphere (r) = 10 cm
Total surface area of hemisphere = 3πr2
= 3 x 3.14 x 10 x 10 = 942 cm2
Hence total surface area of hemisphere is
942 cm2
The radius of a spherical balloonincreases from 7 cm to 14 cm as air isbeing pumped into it. Find the ratio ofsurface areas of the balloon in the two cases.
I case: Radius of balloon (r) = 7 cm
Surface area of balloon = 4πr2
=4π x 7 x 7 cm2……….(i)
II case: Radius of balloon (R) = 14 cm
Surface area of balloon = 4πr2
= 4π x 14 x 14 cm2 …….(ii)
Now, Ratio [from eq. (i) and (ii)],
Hence, required ratio = 1 : 4
A hemispherical bowl made of brass has inner diameter 105 cm. Find the cost of tin-plating it on the inside at the rate of Rs. 16 per 100 cm2.
Inner diameter of bowl
= 10.5 cm
Inner radius of bowl (r) = 10.5/2
= 5.25 cm
Now, Inner surface area of bowl
= 2πr2
=
= Rs. 16
= 
Find the radius of a sphere whose surface area is 154 cm2.
Surface area of sphere = 154 cm2
A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
Inner radius of bowl (r) = 5 cm
Thickness of steel (t) = 0.25 cm
Outer radius of bowl (R) = r + t
= 5 +0.25 = 5.25 cm
Outer curved surface area of bowl
= 173.25 cm2
A right circular cylinder just encloses a sphere of radius r (See figure). Find:
(i) Surface area of the sphere.
(ii) Curved surface area of the cylinder.
(iii) Ratio of the areas obtained in (i) and (ii).
(i) Radius of sphere = r
= 2π(radius)2 = 2πr2
And The radius of cylinder will be equal to radius of sphere.
(ii) 
= 2πrh= 2πr x πr
= 4πr2
So, Required ratio = 1 :1
Exercise 11.5
Find the minimum number of bricks each measuring 22.5 cm x 11.5 cm x 7.5 cm required to construct a wall 10 m long, 6 m high and 1.5 m thick.
Volume of one cuboidal brick
= l x b x h
= 22.5 cm x 11. 5 cm x 7.5 cm3
= 1940.625 cm3
= 0.001940625 m3
Volume of cuboidal wal
= 10 m x 6 m x 1.5 m= 90 m3
Minimum number of bricks required
= 46377 [Since bricks cannot be in fraction]
A matchbox 4 cm x 2.5 cm x 1.5 cm. What will be the volume a packet containing 12 such boxes?
Given: Length (l)= 4 cm, Breadth (b) = 2.5 cm, Height (h) = 1.5 cm
Volume of a matchbox = l x b x h
= 4 x 2.5 x 1.5
= 15 cm3
Volume of a packet containing 12
such matchboxes = 12 x 15 = 180 cm3
A cubical water tank is 6 m long, 5 m wide and 4.5 m deep. How many litres of water can it hold? (1 m3 = 1000 L)
Volume of water in cuboidal tank = 6 m x 5 m x 4.5 m
= 135 m3= 135 x 1000 liters
= 135000 liters
Hence tank can hold 135000 liters of water.
A cuboidal vessel is 10 m long and 8 m wide. How high must it be to hold 380 cubic meters of a liquid?
Let height of cuboidal vessel = 
Volume of liquid in cuboidal vessel
= 380 m3
=> 10 m x 8 m x 
=> 
Hence cuboidal vessel is 4.75 m high.
Find the cost of digging a cuboidal pit 8 m long. 6 m broad and 3 m deep at the rate of Rs. 30 per m3.
Volume of cuboidal pit = 8 m x 6 m x 3 m= 144 m3
Cost of digging 1 m3 cuboidal pit
= Rs. 30
= 30 x 144 = Rs. 4320
he capacity of a cuboidal tank is 50000 litres of water. Find the breadth of the tank, if its length and depth are respectively 2.5 m and 10 m.
(1 m3 = 1000 L)
Capacity of cuboidal tank
= 50000 liters
Hence breadth of cuboidal tank is 2 m.
A village having a population of 4000 requires 150 litres of water per head per day. It has a tank measuring 20 m by 15 m by 6 m. For how many days will the water of this tank last?
Capacity of cuboidal tank
= 1800 m3 = 1800 x 1000 liters
= 1800000 liters
Water required by her head per day
= 150 liters
Water required by 4000 persons per day = 150 x 4000 = 600000 liters
Number of days the water will last
=
= = 3
Hence water of the given tank will last for 3 days.
A godown measures 40 m x 25 m x 15 m. Find the maximum number of wooden crates each measuring 1.5 m x 1.25 m x 0.5 m that can be stored in the godown.
Capacity of cuboidal godown
= 40 m x 25 m x 15 m = 15000 m3
Capacity of wooden crate = 1.5 m x 1.25 m x 0.5 m = 0.9375 m3
Maximum number of crates that can be stored in the godown
=
= = 16000
Hence maximum 16000 crates can be stored in the godown.
A solid cube of side 12 cm is cut into eight cubes of equal volume. What will be the side of the new cube? Also, find the ratio between their surface areas.
Volume of solid cube = (side)3
= (12)3 = 1728 cm3
According to question, Volume of each new cube= 1/8 (Volume of original cube)
= = 216 cm3
Side of new cube = 
Now, Surface area of original solid cube = 6 (side)2
= 6 x 12 x 12 = 864 cm2
Now, Surface area of original solid cube = 6 (side)2= 6 x 6 x 6 = 216 cm2
Now according to the question,
Hence required ration between surface area of original cube to that of new cube = 4 : 1.
A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water eill fall into the sea in a minute?
Since water flows at the rate of 2 km per hour, the water from 2 km of the river flows into the sea in one hour.
Therefore, the volume of water flowing into the sea in one hour
= Volume of a cuboid
= = 2000 m x 40 m x 3 m
= 240000 m3 [1 km = 1000 m]
Now, Volume of water flowing into sea in 1 hour (in 60 minutes)
= 240000 m3
Find the length of a wooden plank of width 2.5 m, thickness 0.025 m and volume 0.25 m3.
Given: Volume of wooden plank
= 0.25 m3
=> lx 2.5 x 0.025 = 0.25
l = 4 m
Hence required length of wooden plank is 4 m.
Exercise 11.6
If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then (i) radius of its base (ii) volume of the cylinder.
Height of the cylinder = 5 cm
Lateral surface area of the cylinder
= 94.2 cm2
=> 2πrh = 94.2
=> 2 x 3.14 x r x 5 = 94.2
= 3 cm
Volume of cylinder = πr2h
= 3.14 x 3 x 3 x 5 = 141.3 cm3
The circumference of the base of a cylindrical vessel is 132 cm and its height is 25 cm. How many litres of water can it hold? (1 m3 = 1000 L)
Height of vessel = h= 25 cm
Circumference of base of vessel
= 132 cm
=>2πr = 132
= 21 cm
Now, Volume of cylindrical vessel
= 
= 
= 34.65 liters
The inner diameter of a cylindrical wooden pipe is 24 cm and its out diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1cm3 of wood has a mass of 0.5 g.
Inner diameter of pipe = 28 cm
Inner radius of pipe (r)
= 24/2 = 12 cm
And Outer diameter of pipe = 28 cm
Outer radius of pipe (R)
= 28/2 = 14 m
Length of pipe (l)= 35 cm
Volume of wood = Volume of outer cylinder – Volume of inner cylinder
= 110 [ 196 – 144 ] = 110 x 52
= 5720 cm3
Weight of 1 cm3 of wood = 0.6 g
Weight of 5720 cm3 of wood
= 0.6 x 5720 = 3432 g = 3.432 kg
A soft drink is available in two packs (i) a tin can with a rectangular base of length 5 cm and width 4 cm, having height of 15 cm (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and how much?
I case: Length of tin 
and Height of tin (h) = 15 cm
Then, Capacity of tin = = 5 x 4 x 15 = 300 cm3
II case: Diameter of base of cylinder = 7 cm
Radius of base of cylinder (r) = 7/2 cm
Height of cylinder = 10 cm
Capacity of cylinder =
= = 385 cm3
From the cases I and II, we observed that
cylindrical container has greater capacity
by (385 – 300) = 85 cm3.
It costs Rs. 2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of Rs. 20 per m2, find:
(i) inner curved surface area of the vessel.
(ii) radius of the base.
(iii) capacity of the vessel.
Solution:
v Total cost to paint inner curved surface area of the vessel = Rs. 2200
Rate = Rs. 20 per square meter
(i) Inner curved surface area of vessel =
= 110 m2
(ii) Depth of the vessel ()= 10 m
Now, Inner surface area of vessel
= 110 m2
= 1.75 m
(iii) Since r = 1.75 m and
= 10 m
Capacity of vessel
= Volume of cylinder = πr2h
= 
= 96.25 kl [1 m3 = 1 kl]
The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square meters of metal sheet would be needed to make it?
Height of the vessel ()= 1 m
Capacity of vessel = 15.4 liters
= 
= 0.0154 m3 [1 m3 = 1 kl]
=> πr2h = 0.0154
=> r2 = 0.0007 x 7 = 0.0048
=> r = 0.07 m
Now, Area of metal sheet required = TSA of cylindrical vessel
= 0.4708 m2
A bag of grain contains 2.8 m3 of grain. How many bags are needed to fill a drum of radius 4.2 m and height 5 m?
Radius of drum (r) = 4.2 m and Height of drum (
Volume of a drum = πr2h
=
= 22 x 0.6 x 4.2 x 5 = 277.2 m3
Now, Number of bags
=
= = 99
Hence 99 bags are needed to fill the drum.
A lead pencil consists of a cylinder of wood with a solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and diameter of graphite is 1 mm. If the length of the pencil is 14 cm, find the columns of the wood and that of the graphite.
Diameter of graphite = 1 mm
Radius of drum = 0.5 mm
= 0.05 cm
Height of graphite ()= 14 cm
Volume of graphite = πr2h
= = 0.11 cm3
Diameter of pencil = 7 mm
Radius of pencil (R) = 3.5 mm
= 0.35 cm
Volume of pencil=
= = 5.39 cm3
Now, Volume of wood = Volume of pencil – Volume of graphite
= 5.39 – 0.11 = 5.28 cm3
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
Diameter of circular base of cylindrical bowl = 7 cm
Radius of circular base of cylindrical
bowl (r)= 7/2 cm
Height of the bowl ()= 4 cm
Now, Volume of cylindrical bowl = πr2h
= = 22 x 7 = 154 cm3
Quantity of soup filled in a bowl
= 154 cm3
Therefore, total quantity of soup to be prepared by the hospital = 250 x 154
= 38500 cm3
= liter [1 liter = 1000 cm3]
= 38.5 liters
Exercise 11.7
Find the capacity of a conical vessel with:
(i) Radius 7 cm, Slant height 25 cm
(ii) Height 12 cm, Slant height 13 cm
(i) Given: r = 7 cm, l = 25 cm
= 24 cm
Capacity of conical vessel =
= = 1232 cm3
= 1.232 liters [1000 cm3= 1liter]
(ii) Given: 
= 5 cm
Capacity of conical vessel =
= = 
= 
[1000 cm3= 1liter]
= 
Find the volume of the right circular cone with:
(i) Radius 6 cm, Height 7 cm
(ii) Radius 3.5 cm, Height 12 cm
(i) Given: r = 6 cm, = 7 cm
Volume of cone =
=
= 264 cm3
(ii) Given: r= 3.5 cm, = 12 cm
Volume of cone =
=
= 154 cm3
The height of a cone is 15 cm. If its volume is 1570 cm3, find the radius of the base. (Use π = 3.14)
Height of the cone 
Volume of cone = 1570 cm3
Hence required radius of the base is 10 cm.
If the volume of a right circular cone of height 9 cm is 48π cm3, find the diameter of the base.
Height of the cone (
Volume of cone = 48π cm3
r = 4 cm
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kiloliters?
Diameter of pit = 3.5 m
Radius of pit (r)= 3.5/2 = 1.75 m
Depth of pit 
Capacity of pit =
= 
= 38.5 kl [1 m3 = 1 kl]
The volume of a right circular cone is 9856 cm3. If the diameter of the base if 28 cm, find:
(i) Height of the cone
(ii) Slant height of the cone
(iii) Curved surface area of the cone.
(i) Diameter of cone = 28 cm
Volume of cone = 9856 cm3
= 9856
(ii) Slant height of cone =
= 50 cm
(iii) Curved surface area of cone = πrl = 
A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained. (Use π = 3.14 )
When right angled triangle ABC is revolved about side 12 cm, then the solid formed is a cone.
In that cone, Height () = 12 cm
And radius (r) = 5 cm
Therefore, Volume of cone =
=
= 100π cm3
If the triangle ABC in question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find, also, the ratio of the volume of the two solids obtained.
When right angled triangle ABC is revolved about side 5 cm, then the solid formed is a cone.
In that cone, Height ()= 5 cm
And radius ( r )= 12 cm
Therefore, Volume of cone =
=
= 240π cm3
Now,
=
Required ratio = 5 : 12
Find the volume of the largest right circular cone that can be fitted in a cube whose edge is 14 cm.
Since, diameter of the largest right circular cone that can be fitted in a cube = Edge of cube
And also Height of the cone 
Now, Volume of the largest cone
=
= 718.66 cm3
A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
Radius (r) of heap
Height (h) of heap = 3 m
Volume of heap
=
Therefore, the volume of the heap of wheat is 86.625 m3.
Area of canvas required = CSA of cone
Therefore, 99.825 m2canvas will be required to protect the heap from rain.
Exercise 11.8
The diameter of the moon is approximately one-fourth the diameter of the earth. What fraction is the volume of the moon of the volume of the earth?
Let diameter of earth be x
Radius of earth (r) = x/2
Now, Volume of earth =
[Earth is considered to be a sphere]
= 
According to question,
Diameter of moon = 
Radius of moon (R) =
Now, Volume of Moon =
[Moon is considered to be a sphere]
[From eq. (i)]
So, Volume of moon is 
Find the volume of a sphere whose radius is (i) 7 cm and (ii) 0.63 cm.
Radius of sphere ( r )= 7 cm
Volume of sphere =
=
= cm3
(ii) Radius of sphere ( r )= 0.63 m
Volume of sphere =
= 1.047816 m3 = 1.05 m3 (approx.)
Find the amount of water displaced by a solid spherical ball of diameter:
(i) 28 cm
(ii) 0.21 m
(i) Diameter of spherical ball
= 28 cm
Radius of spherical ball ( r) = 28/2
= 14 cm
According to question, Volume of water replaced = Volume of spherical ball
=
=
= cm3
(ii) Diameter of spherical ball = 0.21 m
Radius of spherical ball (r)= 0.21/2m
According to question,
Volume of water replaced = Volume of spherical ball
=
= 0.004851 m3
The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the metal weighs 8.9 g per cm3?
Diameter of metallic ball = 4.2 cm
Radius of metallic ball (r)= 4.2/2
= 2.1 cm
Volume of metallic ball =
= 38.808 cm3
Density of metal = 8.9 g per cm3
Mass of 1 cm3 = 8.9 g
Mass of 38.808 cm3 = 8.9 x 38.808
= 345.3912 g = 345.39 g (approx).
How many litres of milk can a hemispherical bowl of diameter 10.5 hold?
Diameter of hemispherical bowl
= 10.5 cm
Radius of hemispherical bowl ( r )
= 
Volume of milk in hemispherical bowl
= 0.303187 liters
= 0.303 liters (approx.)
A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
Inner radius of hemispherical tank ( r ) = 1 m = 100 cm
Thickness of sheet = 1 cm
Outer radius of hemispherical tank (R) = 100 + 1 = 101 cm
Volume of iron of hemisphere
= 63487.81 cm3
= 0.06348 m3
Find the volume of a sphere whose surface area is 154 cm2.
Surface area of sphere = 154 cm2
Now, Volume of sphere
A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of Rs. 498.96. If the cost of white-washing is at the rate of Rs. 2.00 per square meter, find:
(i) the inner surface area of the dome.
(ii) the volume of the air inside the dome.
Cost of white washing from inside = Rs. 498.96
Rate of white washing = Rs. 2
Area white washed
= = 249.48 cm2
Inside surface area of the dome
= 249.48 cm2
= 5.67 x 7
So, Volume of the dome
=
= 523.9 cm3
Twenty seven solid iron spheres, each of radius and surface area S are melted to form a sphere with surface area S’. Find the:
(i) radius r' of the new sphere.
(ii) ratio of S and S’.
(i) Let radius of sphere be r and radius of new sphere be R.
27 x Volume of sphere = Volume of new sphere
A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule?
Diameter of spherical capsule = 3.5 mm
Radius of spherical capsule ( r )
= mm
Medicine needed to fill the capsule
= Volume of sphere =
= 22.46 mm3 (Approx.)
Exercise 11.9
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm [See fig.]. The thickness of the planks is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
External faces to be polished
= Area of six faces of cuboidal bookshelf – 3 (Area of open portion ABCD)
= 2 (110 x 25 + 25 x 85 + 85 x 110) – 3 (75 x 30)
[AB = 85 – 5 – 5 = 75 cm and AD
= [⅓ x 110 – 5 – 5 – 5 – 5 = 30 cm]
= 2 (2750 + 2125 + 9350) – 3 x 2250
= 2 x 14225 – 6750
= 28450 – 6750
= 21700 cm2
Now, cost of painting outer faces of wodden bookshelf at the rate of 20 paise.
= Rs. 0.20 per cm2 = Rs. 0.20 x 21700 = Rs. 4340
Here, three equal five sides inner faces.
Therefore total surface area
= 3 [ 2 (30 + 75) 20 + 30 x 75] [Depth = 25 – 5 = 20 cm]
= 3 [ 2 x 105 x 20 + 2250] = 3
[ 4200 + 2250]
= 3 x 6450 = 19350 cm2
Now, cost of painting inner faces at the rate of 10 paise i.e. Rs. 0.10 per cm2.
= Rs. 0.10 x 19350 = Rs. 1935
Total expenses required = Rs. 4340 + Rs. 1935 = Rs. 6275
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in figure. Eight such spheres are used for this purpose and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find he cost of paint required if silver paint costs 25 paise per cm2 and black paint costs 5 paise per cm2.
Diameter of a wooden sphere
= 21 cm.
Radius of wooden sphere ( R )
= 21/2 cm
And Radius of the cylinder ( r )
= 1.5 cm
Surface area of silver painted part
= Surface area of sphere – Upper part of cylinder for support
= 1378.928 cm2
Surface area of such type of 8 spherical part = 8 x 1378.928
= 11031.424 cm2
Cost of silver paint over 1 cm2
= Rs. 0.25
Cost of silver paint over 11031.928 cm2 = 0.25 x 11031.928
= Rs. 2757.85
Now, curved surface area of a cylindrical support = 2πrh
= = 66 cm2
Curved surface area of 8 such cylindrical supports = 66 x 8 = 528 cm2
Cost of black paint over 1 cm2 of cylindrical support = Rs. 0.50
Cost of black paint over 528 cm2 of cylindrical support = 0.50 x 528
= Rs. 26.40
Total cost of paint required
= Rs. 2757.85 + Rs. 26.4
= Rs. 2784.25
If diameter of a sphere is decreased by 25% then what percent does its curved surface area decrease?
Diameter of original sphere
= D = 2R
R = D/2
Curved surface area of original sphere =
According to the question,
Decreased diameter = 25% of D
=
Diameter of new sphere =
Radius of new sphere =
Now, curved surface area of new sphere =
Change in curved surface area
Percent change in the curved surface area
Sameera wants to celebrate the fifth birthday of her daughter with a party. She bought thick paper to make the conical party caps. Each cap is to have a base diameter of 10 cm and height 12 cm. A sheet of the paper is 25 cm by 40 cm and approximately 82% of the sheet can be effectively used for making the caps after cutting. What is the minimum number of sheets of paper that Sameera would need to buy, if there are to be 15 children at the party?
Diameter of base of conical cap
= 10 cm
Radius of conical cap ( r )= 5 cm
Slant height of cone
= 13 cm
Curved surface area of a cap
= πrl = 3.14 x 5 x 13 = 204.1 cm2
Curved surface area of 15 caps
= 15 x 204.1 = 3061.5 cm2
Area of a sheet of paper used for making caps = 25 x 40 = 1000 cm2
82% of sheet is used after cutting
= 82% of 1000 cm2
= 820 cm2
Number of sheet = = 3.73
Hence 4 sheets area needed .
Admissions Open for 2025-26
Frequently Asked Questions
The NCERT solution for Class 9 Chapter 11: Surface Areas and Volume is important as it provides a structured approach to learning, ensuring that students develop a strong understanding of foundational concepts early in their academic journey. By mastering these basics, students can build confidence and readiness for tackling more difficult concepts in their further education.
Yes, the NCERT solution for Class 9 Chapter 11: Surface Areas and Volume is quite useful for students in preparing for their exams. The solutions are simple, clear, and concise allowing students to understand them better. They can solve the practice questions and exercises that allow them to get exam-ready in no time.
You can get all the NCERT solutions for Class 9 Maths Chapter 11 from the official website of the Orchids International School. These solutions are tailored by subject matter experts and are very easy to understand.
Yes, students must practice all the questions provided in the NCERT solution for Class 9 Maths Chapter 11: Surface Areas and Volume as it will help them gain a comprehensive understanding of the concept, identify their weak areas, and strengthen their preparation.
Students can utilize the NCERT solution for Class 9 Maths Chapter 11 effectively by practicing the solutions regularly. Solve the exercises and practice questions given in the solution.