NCERT Solution for Class 9 Maths Chapter-1 Number System
This article offers a comprehensive and detailed guide to mastering the fundamental concepts of real numbers through NCERT Solutions for Class 9 Maths Chapter 1. The step-by-step explanations provided in the article, along with essential study materials, aim to facilitate a thorough understanding of the topic. Chapter 1 of Class 9 Maths NCERT, focusing on rational numbers and their applications, is crucial for not only achieving high academic performance but also for building a strong foundation to grasp subsequent concepts introduced in the eighth grade.
Access Answers to NCERT Solution for Class 9 Maths Chapter-1 Number System
Students can access the NCERT Solution for Class 9 Maths Chapter-1 Number System. Curated by experts according to the CBSE syllabus for 2023–2024, these step-by-step solutions make Maths much easier to understand and learn for the students. These solutions can be used in practice by students to attain skills in solving problems, reinforce important learning objectives, and be well-prepared for tests.
Exercise 1.1
Is zero a rational number? Can you write it in the form p/q where p and q are integers and q ≠ 0?
We know that a number is said to be rational if it can be written in the form p/q, where p and q are integers and q ≠ 0.
Taking the case of ‘0’, Zero can be written in the form 0/1, 0/2, 0/3 … as well as , 0/1, 0/2, 0/3 .. Since it satisfies the necessary condition, we can conclude that 0 can be written in the p/q form, where q can either be positive or negative number.
Hence, 0 is a rational number.
Find six rational numbers between 3 and 4.
There are infinite rational numbers between 3 and 4.
As we have to find 6 rational numbers between 3 and 4, we will multiply both the numbers, 3 and 4, with 6+1 = 7 (or any number greater than 6) i.e., 3 × (7/7) = 21/7 and, 4 × (7/7) = 28/7. The numbers in between 21/7 and 28/7 will be rational and will fall between 3 and 4.
Hence, 22/7, 23/7, 24/7, 25/7, 26/7, 27/7 are the 6 rational numbers between 3 and 4.
Find five rational numbers between 3/5 and 4/5.
There are infinite rational numbers between 3/5 and 4/5. To find out 5 rational numbers between 3/5 and 4/5, we will multiply both the number 3/5 and 4/5 with 5+1=6 (or any number greater than 5)
i.e., (3/5) × (6/6) = 18/30 and,
(4/5) × (6/6) = 24/30
The numbers in between 18/30 and 24/30 will be rational and will fall between 3/5 and 4/5.
Hence,19/30, 20/30, 21/30, 22/30, 23/30 are the 5 rational numbers between 3/5 and ⅘
State whether the following statements are true or false. Give reasons for your answers.
(i) Every natural number is a whole number.
(ii) Every integer is a whole number.
(iii) Every rational number is a whole number.
(i) True
Natural numbers- Numbers starting from 1 to infinity (without fractions or decimals)
i.e., Natural numbers = 1,2,3,4…
Whole numbers – Numbers starting from 0 to infinity (without fractions or decimals)
i.e., Whole numbers = 0,1,2,3…
Or, we can say that whole numbers have all the elements of natural numbers and zero. Every natural number is a whole number; however, every whole number is not a natural number.
(ii) False
Integers- Integers are set of numbers that contain positive, negative and 0; excluding fractional and decimal numbers.
i.e., integers= {…-4,-3,-2,-1,0,1,2,3,4…}
Whole numbers- Numbers starting from 0 to infinity (without fractions or decimals)
i.e., Whole numbers= 0,1,2,3….
Hence, we can say that integers include whole numbers as well as negative numbers. Every whole number is an integer; however, every integer is not a whole number.
(iii) False
Rational numbers- All numbers in the form p/q, where p and q are integers and q≠0.
i.e., Rational numbers = 0, 19/30 , 2, 9/-3, -12/7…
Whole numbers- Numbers starting from 0 to infinity (without fractions or decimals)
i.e., Whole numbers= 0,1,2,3….
Hence, we can say that integers include whole numbers as well as negative numbers. All whole numbers are rational, however, all rational numbers are not whole numbers.
Exercise 1.2
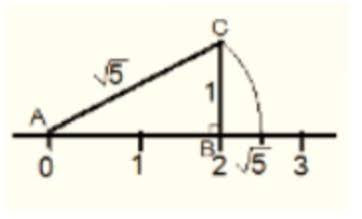
Show how √5 can be represented on the number line.
Step 1: Let line AB be of 2 unit on a number line.
Step 2: At B, draw a perpendicular line BC of length 1 unit.
Step 3: Join CA
Step 4: Now, ABC is a right angled triangle. Applying Pythagoras theorem,
AB2+BC2 = CA2
2*2+1*2 = 5
⇒ CA = √5 .
Thus, CA is a line of length √5 unit.
Step 4: Taking CA as a radius and A as a center draw an arc touching the number line. The point at which number line get intersected by arc is at √5 distance from 0 because it is a radius of the circle whose center was A.
Thus, √5 is represented on the number line as shown in the figure.
State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form √m where m is a natural number.
(iii) Every real number is an irrational number.
(i) True
Irrational Numbers – A number is said to be irrational, if it cannot be written in the p/q, where p and q are integers and q ≠ 0.
i.e., Irrational numbers = π, e, √3, 5+√2, 6.23146…. , 0.101001001000….
Real numbers – The collection of both rational and irrational numbers are known as real numbers.
i.e., Real numbers = √2, √5, π, 0.102…
Every irrational number is a real number, however, every real number is not an irrational number.
(ii) False
The statement is false since as per the rule, a negative number cannot be expressed as square roots.
E.g., √9 =3 is a natural number. But √2 = 1.414 is not a natural number.
Similarly, we know that there are negative numbers on the number line, but when we take the root of a negative number it becomes a complex number and not a natural number.
E.g., √-7 = 7i, where i = √-1 The statement that every point on the number line is of the form √m, where m is a natural number is false.
(iii) False
The statement is false. Real numbers include both irrational and rational numbers. Therefore, every real number cannot be an irrational number.
Real numbers – The collection of both rational and irrational numbers are known as real numbers. i.e., Real numbers = √2, √5, , 0.102…
Irrational Numbers – A number is said to be irrational, if it cannot be written in the p/q, where p and q are integers and q ≠ 0. i.e., Irrational numbers = π, e, √3, 5+√2, 6.23146…. , 0.101001001000….
Every irrational number is a real number, however, every real number is not irrational.
Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
No, the square roots of all positive integers are not irrational.
For example, √4 = 2 is rational. √9 = 3 is rational.
Hence, the square roots of positive integers 4 and 9 are not irrational. ( 2 and 3, respectively).
Classroom activity (Constructing the ‘square root spiral’) : Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP1 of unit length. Draw a line segment P1P2 perpendicular to OP1 of unit length (see Fig. 1.9). Now draw a line segment P2P3 perpendicular to OP2. Then draw a line segment P3P4 perpendicular to OP3. Continuing in Fig. 1.9 :
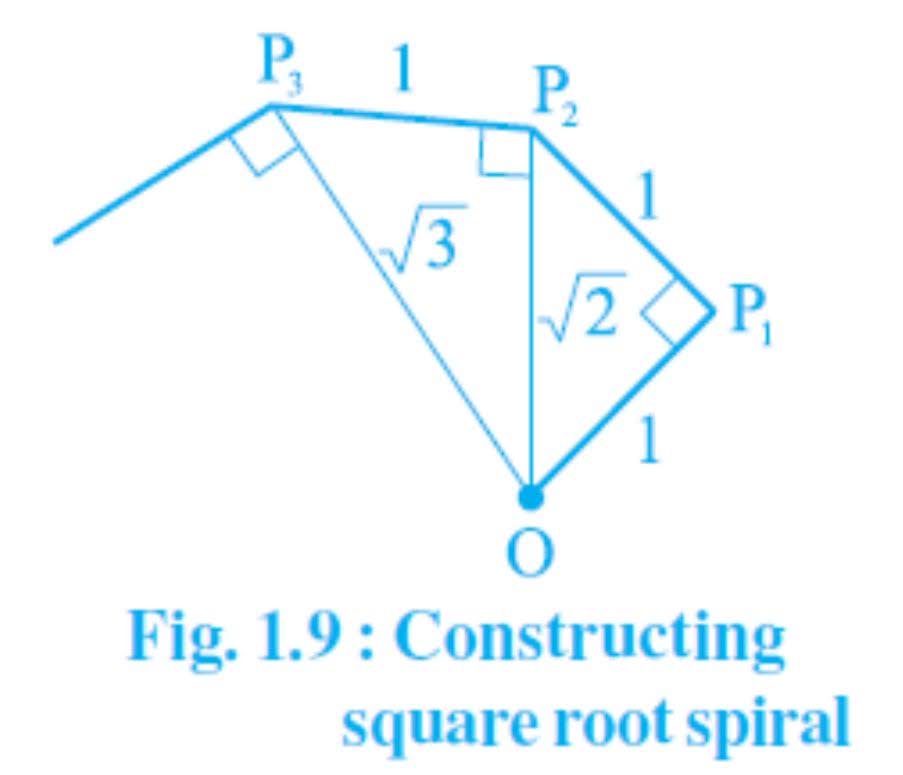
Constructing this manner, you can get the line segment Pn-1Pn by square root spiral drawing a line segment of unit length perpendicular to OPn-1. In this manner, you will have created the points P2, P3,….,Pn,… ., and joined them to create a beautiful spiral depicting √2, √3, √4, …
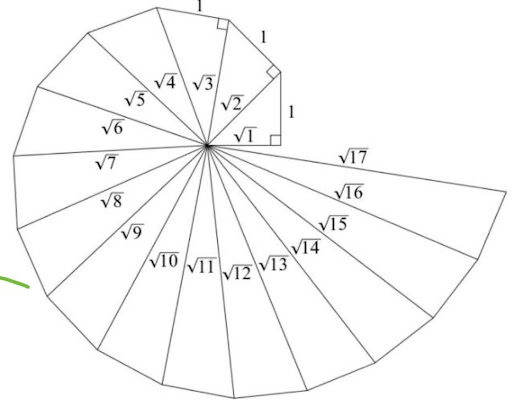
Step 1: Mark a point O on the paper. Here, O will be the center of the square root spiral.
Step 2: From O, draw a straight line, OA, of 1 cm horizontally.
Step 3: From A, draw a perpendicular line, AB, of 1 cm.
Step 4: Join OB. Here, OB will be of √2
Step 5: Now, from B, draw a perpendicular line of 1 cm and mark the end point C.
Step 6: Join OC. Here, OC will be of √3
Step 7: Repeat the steps to draw √4, √5, √6….
Exercise 1.3
Write three numbers whose decimal expansions are non-terminating non-recurring.
√2 = 1.414213562 ………..
√3 = 1.732050808 …….
√5 = 2.23606797 …….
Write the following in decimal form and say what kind of decimal expansion each has :
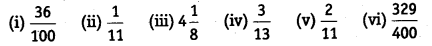
(i) We have,
36/100= 0.36
Thus, the decimal expansion of 36/100 is terminating.
(ii) Dividing 1 by 11, we have
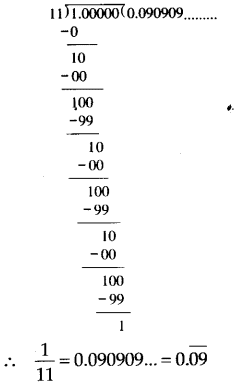
Thus, the decimal expansion of 1/11 is non-terminating repeating.

Dividing 33 by 8, we get
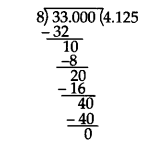
= 4.125. Thus, the answer is terminating.
(iv)3/13
Dividing 3 by 13, we get

Here, the repeating block of digits is 230769
∴ 3/13 = 0.23076923…
Thus, the decimal expansion of 3/13 is non-terminating repeating.
(v) 2/11
Dividing 2 by 11, we get
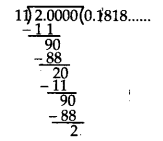
Here, the repeating block of digits is 18.
∴ 2/11 = 0.1818… = 0.18
Thus, the decimal expansion of 2/11 is non-terminating repeating.
(vi)329/400
Dividing 329 by 400, we get

∴ 329/400 = 0.8225. Thus, the decimal expansion of 329/400is terminating.
You know that 1/7 = 0.142857. Can you predict what the decimal expansions of 2/7, 3/7, 4/7, 5/7, 6/7 are, without actually doing the long division? If so, how? [Hint: Study the remainders while finding the value of 1/7 carefully.]
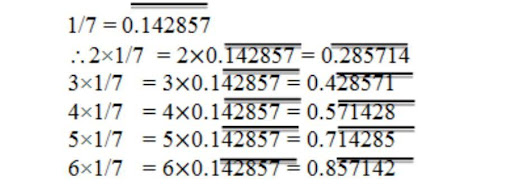
Express the following in the form p/q, where p and q are integers and q 0.
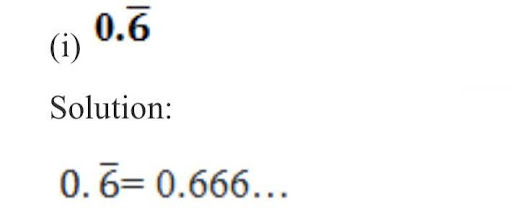
Solution: Assume that x = 0.666…
Then ,10x = 6.666…
10x = 6 + x
9x = 6
x = ⅔
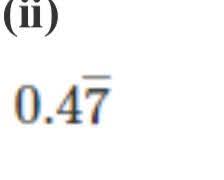

= (4/10)+(0.777/10)
Assume that x = 0.777…
Then, 10x = 7.777…
10x = 7 + x
x = 7/9
(4/10)+(0.777../10) = (4/10)+(7/90) ( x = 7/9 and x = 0.777…0.777…/10 = 7/(9×10) = 7/90 )
= (36/90)+(7/90) = 43/90

Assume that x = 0.001001…
Then, 1000x = 1.001001…
1000x = 1 + x
999x = 1
x = 1/999
Express 0.99999…. in the form p/q . Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Assume that,
x = 0.9999…..Eq (a)
Multiplying both sides by 10,
10x = 9.9999…. Eq. (b)
Eq.(b) – Eq.(a), we get
10x = 9.9999 –x = -0.9999…
_____________
9x = 9
x = 1
The difference between 1 and 0.999999 is 0.000001 which is negligible.
Hence, we can conclude that, 0.999 is very near 1, therefore, 1 as the answer can be justified.
What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 1/17 ? Perform the division to check your answer.
1/17
Dividing 1 by 17:
Dividing 1 by 17, we have

The remainder I is the same digit from which we started the division.
∴ 1/17= 0.0588235294117647
Thus, there are 16 digits in the repeating block in the decimal expansion of 1/17.
Hence, our answer is verified.
Look at several examples of rational numbers in the form p/q (q ≠ 0). Where, p and q are integers with no common factors other that 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Let us look decimal expansion of the following terminating rational numbers:


We observe that the prime factorisation of q (i.e. denominator) has only powers of 2 or powers of 5 or powers of both.
Find three different irrational numbers between the rational number 5/7 and 9/11.
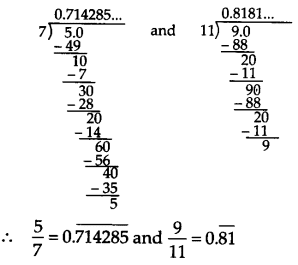
We have,
Three irrational numbers between 0.714285 and 0.81 are
(i) 0.750750075000 …..
(ii) 0.767076700767000 ……
(iii) 0.78080078008000 ……
Classify the following numbers as rational or irrational
(i) √23
(ii) √225
(iii) 0.3796
(iv) 7.478478…..
(v) 1.101001000100001………
(i) ∵ 23 is not a perfect square.
∴ √23 is an irrational number.
(ii) ∵ 225 = 15 x 15 = 152
∴ 225 is a perfect square.
Thus, √225 is a rational number.
(iii) ∵ 0.3796 is a terminating decimal.
∴ It is a rational number.
(iv) 7.478478
The number,7.478478, is non-terminating but recurring
∴ It is a rational number.(v) Since, 1.101001000100001… is a non terminating, non-repeating decimal number.
∴ It is an irrational number.
Exercise 1.4
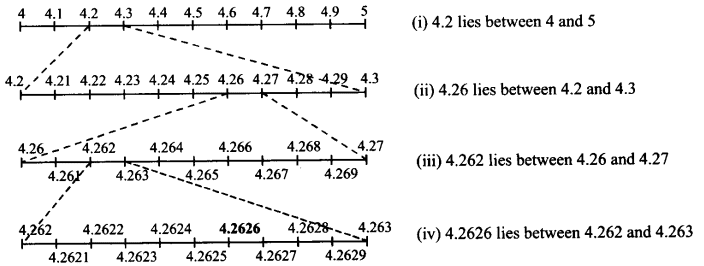
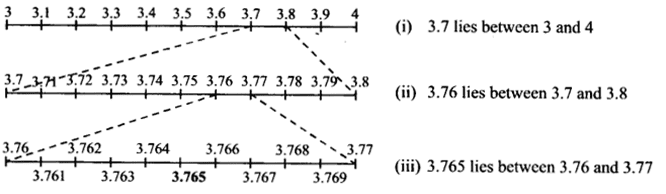
Visualise 4.26¯ on the number line, upto 4 decimal places.
4.2626 lies between 4 and 5.
Visualise 3.765 on the number line, using successive magnification.
3.765 lies between 3 and 4.
Exercise 1.5
Rationalize the denominator of the following
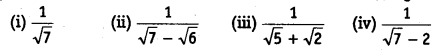
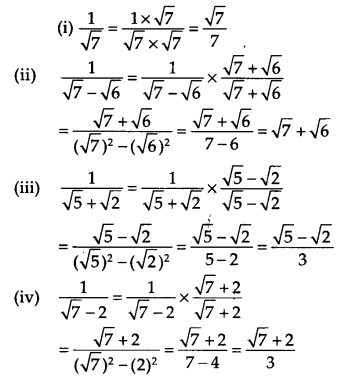
Classify the following numbers as rational or irrational.
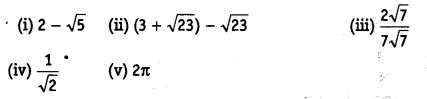
(i) Since, it is a difference of a rational and an irrational number.
∴ 2 – √5 is an irrational number.
(ii) 3 + √23- √23
(3 +√23) –√23 = 3+√23–√23
= 3
= 3/1
Since the number 3/1 is in p/q form, (3 +√23)- √23 is rational
which is a rational number.
(iii) 2√7/7√7
Solution: 2√7/7√7 = ( 2/7)× (√7/√7)
We know that (√7/√7) = 1
Hence, ( 2/7)× (√7/√7) = (2/7)×1 = 2/7
Since the number, 2/7 is in p/q form, 2√7/7√7 is rational. , which is a rational number.
(iv) 1/√2
Solution: Multiplying and dividing numerator and denominator by √2 we get,
(1/√2) ×(√2/√2)= √2/2 ( since √2×√2 = 2)
We know that, √2 = 1.4142…
Then, √2/2 = 1.4142/2 = 0.7071..
Since the number, 0.7071..is non-terminating non-recurring, 1/√2 is an irrational number.
(v) 2
Solution: We know that, the value of = 3.1415(v)
∵ 2π = 2 x π = Product of a rational and an irrational number is an irrational number.
∴ 2π is an irrational number.
Simplify each of the following expressions

(i) (3 + √3)(2 + √2)
= 2(3 + √3) + √2(3 + √3)
= 6 + 2√3 + 3√2 + √6
Thus, (3 + √3)(2 + √2) = 6 + 2√3 + 3√2 + √6
(ii) (3 + √3)(3 – √3) = (3)2 – (√3)2
= 9 – 3 = 6
Thus, (3 + √3)(3 – √3) = 6
(iii) (√5 + √2)2 = (√5)2 + (√2)2 + 2(√5)(√2)
= 5 + 2 + 2√10 = 7 + 2√10
Thus, (√5 + √2 )2 = 7 + 2√10
(iv) (√5 – √2)(√5 + √2) = (√5)2 – (√2)2 = 5 – 2 = 3
Thus, (√5 – √2) (√5 + √2) = 3
Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is π = c/d. This seems to contradict the fact that n is irrational. How will you resolve this contradiction?
When we measure the length of a line with a scale or with any other device, we only get an approximate ational value, i.e. c and d both are irrational.
∴ c/d is irrational and hence π is irrational.
Thus, there is no contradiction in saying that it is irrational.
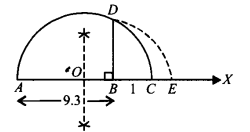
Represent √9.3 on the number line.
Draw a line segment AB = 9.3 units and extend it to C such that BC = 1 unit.
Find mid point of AC and mark it as O.
Draw a semicircle taking O as centre and AO as radius. Draw BD ⊥ AC.
Draw an arc taking B as centre and BD as radius meeting AC produced at E such that BE = BD = √9.3 units.
Exercise 1.6
Find:
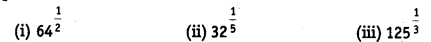
(i) 64 = 8 x 8 = 82
∴ (64)1/2 = (82)1/2 = 82 x 1/2 = 8 [(am)n = am x n]
(ii) 32 = 2 x 2x 2 x 2 x 2 = 25
∴ (32)1/5= (25)1/5= 25 x 1/5 = 2 [(am)n= am x n]
(iii) 125 = 5 x 5 x 5 = 53
∴ (125)1/3 = (53)1/3 = 53 x 1/3 = 5 [(am)n = am x n]
Find:
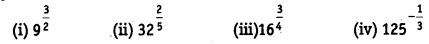
(i) 9 = 3 x 3 = 32
∴ (9)3/2= (32)3/2 = 32 x 3/2 = 33 = 27
[(am)n = amn]
(ii) 32 = 2 x 2 x 2 x 2 x 2= 25
∴ (32)2/5 = (25)2/5 = 25 x 2/5 = 22 = 4
[(am)n = amn]
(iii) 16 = 2 x 2 x 2 x 2 = 24
∴ (16)3/4 = (24)3/4 = 24 x 3/4 = 23 = 8
[(am)n = amn]
(iv) 125 = 5 x 5 x 5 = 53
∴ (125)-1/3 = (53)-1/3 = 53 x (-1/3) = 5-1
=1/5
Simplify:
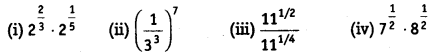
(i) 22/3. 21/5 = 22/3 + 1/5 = 213/15
[am. an = am + n
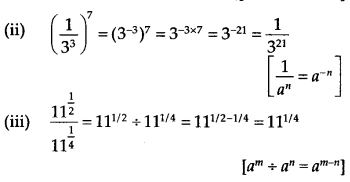
(iv) 71/2.81/2 = (7 x 8)1/2 = (56)1/2 [am x bm = (ab)m]
Admissions Open for 2025-26
Frequently Asked Questions
The NCERT solution for Class 9 Chapter 1: Number System is important as it provides a structured approach to learning, ensuring that students develop a strong understanding of foundational concepts early in their academic journey. By mastering these basics, students can build confidence and readiness for tackling more difficult concepts in their further education.
Yes, the NCERT solution for Class 9 Chapter 1: Number System is quite useful for students in preparing for their exams. The solutions are simple, clear, and concise allowing students to understand them better. They can solve the practice questions and exercises that allow them to get exam-ready in no time.
You can get all the NCERT solutions for Class 9 Maths Chapter 1 from the official website of the Orchids International School. These solutions are tailored by subject matter experts and are very easy to understand.
Yes, students must practice all the questions provided in the NCERT solution for Class 9 Maths Chapter 1: Number System as it will help them gain a comprehensive understanding of the concept, identify their weak areas, and strengthen their preparation.
Students can utilize the NCERT solution for Class 9 Maths Chapter 1 effectively by practicing the solutions regularly. Solve the exercises and practice questions given in the solution.

