NCERT Solutions for Class 11 Chemistry Chapter 6 Equilibrium
Looking for reliable NCERT Solutions for Class 11 Chemistry? Here comes the aid from Orchids International School, with a well-structured solution that will help you in simplifying those complex concepts. Be it the fundamentals of Class 11 Equilibrium or the minute details in class 11 chemistry part 1 chapter 6, Orchids ensures that you're following the right guideline throughout your studies. Understanding equilibrium is the real foundation for so many higher-level chemistry concepts. At the end, access our class 11 chemistry part 1 chapter 6 PDF to help give your studies a boost.
Access Answers to NCERT Solutions for Class 11 Chemistry Chapter 6 Equilibrium
Students can access the NCERT Solutions for Class 11 Chemistry Chapter 6 Equilibrium. Curated by experts according to the CBSE syllabus for 2023–2024, these step-by-step solutions make Chemistry much easier to understand and learn for the students. These solutions can be used in practice by students to attain skills in solving problems, reinforce important learning objectives, and be well-prepared for tests.
Equilibrium
At 450K, Kp=2.0×10^10bar - 1 for the given reaction reaction at equilibrium. 2SO2(g)+O2(g)⇌2SO3(g) , What is Kc at this temperature?
For the given reaction:
Δn=2−3=−1
T=450K
R=0.0831bar L bar K−1mol−1
Kp=2.0×10^10bar−1
We know that,
Kp=Kc(RT)Δn
2.0×1010=Kc(0.0831×450)−1
Kc=2.0×1010(0.0831×450)
Kc=74.79×1014Lmol
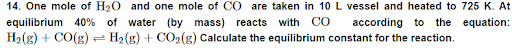



A liquid is in equilibrium with its vapour in a sealed container at a fixed temperature. The volume of the container suddenly increased.
1. What is the initial effect of the change on vapour pressure?
Ans: The vapour pressure would first fall if the container's volume was rapidly increased. This is due to the fact that the amount of vapour remains constant while the volume increases rapidly. As a result, the same amount of vapour is spread over a wider surface area.
2. How do rates of evaporation and condensation change initially?
Ans: The rate of evaporation is also constant because the temperature is constant. The density of the vapour phase reduces as the container volume increases. As a result, the rate of vapour particle collisions drops as well. As a result, the rate of condensation initially slows.
3. What happens when equilibrium is restored finally and what will be the final vapour pressure?
Ans: The rate of evaporation equals the rate of condensation when equilibrium is eventually restored. Only the volume changes in this situation, but the temperature remains fixed. Temperature, not volume, determines vapour pressure. As a result, the final vapour pressure will be the same as the system's initial vapour pressure.
What is Kc for the following equilibrium when the equilibrium concen -tration of each substance is:
[SO2]=0.60M , [O2]=0.82M and [SO3]=1.90M ? 2SO2(g)+O2(g)⇌2SO3(g)
The equilibrium constant for the given reaction will be:
Kc=[SO3]2 / [SO2]2[O2] =(1.90)2M2 / (0.60)2(0.821)M3
Kc=12.239M−1 (approximately)
Therefore, the equilibrium constant for the given reaction is 12.239M−1.
At a certain temperature and total pressure of 105 Pa, iodine vapour contains 40% by volume of iodine atoms. I2(g)⇌2I (g) . Calculate KP for the equilibrium.
Write the expression for the equilibrium constant, Kc for each of the following reactions:
Find out the value of for each of the following equilibria from the value of :

For the following equilibrium, Kc=6.3×1014 at 1000K
NO (g)+O3(g)⇌NO2(g)+O2(g) Both the forward and reverse reactions in the equilibrium are elementary bimolecular reactions. What is Kc for the reverse reaction?
According to the question: The Kc for the forward reaction is 6.3×1014
Then, Kc for the reverse reaction will be:
K'c=1/ Kc
K'c=1/ 6.3×1014
K'c=1.59×10−15
The equilibrium constant for the reverse reaction will be:
1.59×10−15.
Explain why pure liquids and solids can be ignored while writing the equilibrium constant expression?
For a pure substance which is both a solid and a liquid:
[Pure substance]=Number of molesVolume
[Pure substance]=Mass / Molecular weightVolume
[Pure substance]=MassVolume × Molecular mass
[Pure substance]=DensityMolecular mass
The molecular mass and density of a pure substance (at a given temperature) are now always fixed and accounted for in the equilibrium constant. As a result, the equilibrium constant statement does not include the values of pure substances.
Reaction between nitrogen and oxygen takes place as follows:
2N2(g)+O2(g)⇌2N2O (g) If a mixture of 0.482 mol of N2 and 0.933 mol of
O2 is placed in a 10 L reaction vessel and allowed to form N2O at a temperature for which Kc=2.0×10−37 , determine the composition of equilibrium mixture.
Let the concentration of N2O at equilibrium be x.
The initial concentration of N2 is 0.482mol.
The initial concentration of O2 is 0.933mol.
At equilibrium the concentration of N2 is (0.482-x)mol, the concentration of
O2is (0.933-x)mol and the concentration of N2O is x mol.
The reaction occurs in a 10L reaction vessel:
[N2]=0.482−x/10 , [O2]=0.933−x/2 /10 , [N2O]=x/10
The value of equilibrium constant i.e.
Kc=2.0×10−37 is very small. Therefore, the amount of nitrogen and oxygen reacted is also very small. Thus, x can be neglected from the expressions of molar concentrations of nitrogen and oxygen. Then,
Nitric oxide reacts with Br2 and gives nitrosyl bromide as per reaction given below:
2NO (g)+Br2(g)⇌2NOBr (g) When 0.087 mol of NO and 0.0437 mol of
Br2 are mixed in a closed container at constant temperature, 0.0518 mol of
NOBr is obtained at equilibrium. Calculate equilibrium amount of NO and
Br2 .
The given reaction is:
2NO (g)+Br2(g)⇌2NOBr (g)
Now, 2 mol of NOBr are formed from 2 mol of NO . Therefore, 0.0518 mol of
NOBr are formed from 0.0518 mol of NO. Again, 2 mol of NOBr are formed from 1 mol of Br . Therefore, 0.0518 mol of NOBr are formed from 0.0581 /2 mol of
Br, or 0.0259 mol of NO. The amount of NO and Br present initially is as follows:
[NO]=0.087mol and [Br2]=0.0437mol
Therefore, the amount of NO present at equilibrium is:
[NO]=0.087−0.0518=0.0352mol And, the amount of Br present at equilibrium is:
[Br2]=0.0437−0.0259=0.0178mol
A sample of HI (g) is placed in flask at a pressure of 0.2 atm. At equilibrium the partial pressure of HI (g) is 0.04 atm. What is Kp for the given equilibrium? 2HI (g)⇌H2(g)+I2(g)
The initial concentration of HI is 0.2 atm. At equilibrium, it has a partial pressure of 0.04 atm. Therefore, a decrease in the pressure of HI is 0.2 – 0.04 = 0.16. The given reaction is:
A mixture of 1.57 mol of N2 , 1.92 mol of H2 and 8.13 mol of NH3 is introduced into a 20 L reaction vessel at 500 K. At this temperature, the equilibrium constant, Kc for the reaction is 1.7×102 . The reaction is:
N2(g)+3H2(g)⇌2NH3(g) . Is the reaction mixture at equilibrium? If not, what is the direction of the net reaction?
For the given reaction:
N2(g)+3H2(g)⇌2NH3(g)
The given concentration of various species is
[N2]=1.57/ 20molL−1 [H2]=1.92/ 20molL−1
[NH3]=8.13/ 20molL−1
Now, reaction quotient Qc is:
QC=[NH3]^ /2[N2][H2]^3
QC=((8.13)20)^2 /(1.5720)(1.9220)^3
QC=2.4×103
Since, 𝑄𝑐 ≠ 𝐾𝑐, the reaction mixture is not at equilibrium.
Again, 𝑄𝑐 >𝐾𝑐. Hence, the reaction will proceed in the reverse direction
The equilibrium constant for the following reaction is 1.6×105 at 1024K.
H2(g)+Br2(g)⇌2HBr (g) , Find the equilibrium pressure of all gases if 10.0 bar of HBr is introduced into a sealed container at 1024 K.
Given,
Kp for the reaction i.e.,
H2(g)+Br2(g)↔2HBr(g) is 1.6×105
Equilibrium constant, Kc for the reaction N2(g)+3H2(g)⇌2NH3(g) at 500 K os 0.061. At a particular time, the analysis shows that composition of the reaction mixture is 3.0 molL−1 , 2.0 molL−1 H2 and 0.5 molL−1 NH3 . Is the reaction at equilibrium? If not in which direction does the reaction tend to proceed to reach equilibrium?
The given reaction is: N2(g)+3H2(g)⇌2NH3(g)
At a particular time, the concentration of N2 is 3.0 molL−1 , for H2 is 2.0 molL−1 and for NH3 is 0.5 molL−1.
Now, we know that:
Qc=[NH3]2[N2][H2]3=(0.5)2(3.0)(2.0)3=0.0104
It is given that Kc=0.061
Since Qc≠Kc , the reaction is not at equilibrium.
Since Qc<Kc , the reaction will proceed in the forward direction to reach equilibrium.
What is the equilibrium concentration of each of the substances in the equilibrium when the initial concentration of ICI was 0.78 M?
2ICI (g)⇌I2(g)+Cl2(g) ; Kc=0.14
Kp=0.04atm at 899 K for the equilibrium shown below. What is the equilibrium concentration of C2H6 when it is placed in a flask at 4.0 atm pressure and allowed to come to equilibrium?
C2H6(g)⇌C2H4(g)+H2(g)
Let p be the pressure exerted by ethene and hydrogen gas (each) at equilibrium. Now, according to the reaction
C2H6(g)⇌C2H4(g)+H2(g)
The initial concentration of C2H6 is 4.0 atm and that of C2H4 and H2 is zero (0).
At equilibrium, the concentration of C2H6 is (4.0 – p) and that of C2H4 and
H2 is p.
Then we can write,
⇒Kpp×p40−p=0.04
p2=0.16−0.04p
p2+0.04p−0.16=0
A sample of pure PCl5 was introduced into an evacuated vessel at 473 K. After equilibrium was attained, concentration of PCl5 was found to be
0.5×10−1molL - 1 . If value of Kc is 8.3×10−3 , what are the concentrations of PCl3 and Cl2 at equilibrium?
PCl5(g)⇌PCl3(g)+Cl2(g)
Let the concentrations of both PCl3 and Cl2 at equilibrium be xmolL - 1 . The given reaction is:
PCl5(g)⇌PCl3(g)+Cl(g)
At equilibrium the concentration of PCl5 is
0.5×10−1molL - 1.
It is given that the value of equilibrium constant Kc is 8.3×10−3
The expression for equilibrium will be:
⇒[PCl3][Cl2] / [PCl5]=Kc
⇒x×x / 0.5×10−1=8.3×10^−3
⇒x2=4.15×10−4
⇒x=2.04×10−2
⇒x=0.0204
Therefore at equilibrium:
[PCl3]=[Cl2]=0.02molL−1
One of the reactions that takes place in producing steel from iron ore is the reduction of iron (II) oxide by carbon monoxide to give iron metal and
FeO (s)+CO (g)⇌Fe (s)+CO2(g) ; Kp=0.0265 at 1050 K. What are the equilibrium partial pressures of CO and CO2 at 1050 K if the initial partial pressures are:
pCO=1.4atm and pCO2=0.80atm ?
For the given reaction:
FeO (s)+CO (g)⇌Fe (s)+CO2(g)
The initial concentration of FeO is 1.4 atm and the initial concentration of
CO2 is 0.80 atm.
It is given in the that, Kp=0.265.
Since Qp>Kp , the reaction will proceed in the backward direction.
Therefore, we can say that the pressure of CO will increase while the pressure of CO2 will decrease. Now, let the increase in pressure of CO be equal to the decrease in pressure of CO2 be ‘p’. Then, we can write:
Qp=pCO2pCO=0.801.4=0.571
Therefore, equilibrium partial of CO2 will be,
pCO2=0.080−0.339=0.461 atm
And, equilibrium partial pressure of CO will be,
pCO=1.4−0.339=1.739 atm
Bromine monochloride, BrCl decomposes into bromine and chlorine and reaches the equilibrium:
2BrCl (g)⇌Br2(g)+Cl2(g) for which Kc=32 at 500 K. If initially pure BrCl is present at a concentration of 3.3×10−3 molL−1 , what is its molar concentration in the mixture at equilibrium?
Let the amount of bromine and chlorine formed at equilibrium be ‘x’. The given reaction is:
2BrCl (g)⇌Br2(g)+Cl2(g)
At equilibrium the concentration of BrCl is(3.3×10−3−2x)
Now, we can write.
⇒[Br2][Cl2][BrCl]=Kc
⇒x×x(3.3×10−3−2x)2=32
⇒x3.3×10−3−2x=5.66
⇒x=18.678×10−3−11.32x
⇒12.32x=18.678×10^−3
⇒x=1.5×10^−3
Therefore, at equilibrium
[BrCl]=3.3×10−3−(2×1.5×10−3)
[BrCl]=3.3×10−3−3.0×10−3
[BrCl]=3.0×10−4 molL−1
At 1127 K and 1 atm pressure, a gaseous mixture of CO and CO2 in equilibrium with solid carbon has 90.55% CO by mass:
C (s)+CO2(g)⇌2CO (g). Calculate Kc for this reaction at the above temperature.
Let, the total mass of the gas mixture = 100 gm
Mass of CO = 90.55 gm
And, mass of CO2 = (100 – 90.55) = 9.45 gm
Now, the number of moles of
nCO=90.5528=3.234 mol
Number of moles of
nCO2=9.4544=0.215 mol
Partial pressure of total pCO=nCOnCO+nCO2×ptotal
pCO=3.2343.234+0.215×1
pCO=0.938atm
Partial pressure of CO2 ,
pCO2=nCO2nCO+nCO2×ptotal
pCO2=0.2153.234+0.215×1
pCO2=0.062 atm
Therefore,
For the given reaction:
Δn=2−1=1
We know that,
Kp=Kc(RT)Δn14.19
=Kc(0.082×1127)1
Kc=14.190.082×1127
Kc=0.154
Calculate:
a. ΔG∘ and
b. The equilibrium constant for the formation of NO2 from NO and O2 at 298 K
NO (g)+12O2(g)⇌NO2(g)
Where:
ΔfG∘(NO2)=52kJ/mol
ΔfG∘(NO)=87.0kJ/mol
ΔfG∘(O2)=0kJ/mol
Ans: For the given reaction:
NO (g)+12O2(g)⇌NO2(g)
1. The ΔG∘ for the given reaction will be:
ΔG∘=ΔG∘(Products)−ΔG∘(Reactants)
ΔG∘=52.0−[87.0+0]
ΔG∘=−35.0 kJmol−1
2. We know that:
ΔG∘=RTlogKc
ΔG∘=2.303RTlogKc
logKc=−35.0×10−^ / 3−2.303×8.314×298
logKc=6.13
Kc=antilog (6.134)
Kc=1.36×106
Hence, the equilibrium constant for the given reaction
Kc is 1.36×106 .
Does the number of moles of reaction products increase, decrease or remain the same when each of the following equilibria is subjected to a decrease in pressure by increasing the volume?
a. PCl5(g)⇌PCl3(g)+Cl2(g)
Ans: The amount of moles produced by the reaction will rise. According to Le Chatelier's principle, as pressure is reduced, the equilibrium swings in the direction of a greater number of moles of gas. The number of moles of gaseous products in the reaction is greater than the number of moles of gaseous reactants. As a result, the reaction will be propelled ahead. As a result, there will be more moles of reaction products.
b. CaO (s)+CO2(g)⇌CaCO3(s)
Ans: When the given equation is subjected to a decrease in pressure the number of moles of reaction products will decrease.
c. 3Fe (s)+4H2O (g)⇌Fe3O4(s)+4H2(g)
Ans: When the given equation is subjected to a decrease in pressure the number of moles of reaction products will remain the same.
Which of the following reactions will get affected by increasing the pressure? Also, mention whether change will cause the reaction to go into forward or backward direction.
-
COCl2(g)⇌CO (g)+Cl2(g)
-
CH4(g)+2S2(g)⇌CS2(g)+2H2S (g)
-
CO2(g)⇌C (s)+2CO (g)
-
2H2(g)+CO (g)⇌CH3OH (g)
-
CaCO3(s)⇌CaO (s)+CO2(g)
-
4NH3(g)+5O2(g)⇌4NO (g)+6H2O (g)
By increasing the pressure, the reactions in (i), (iii), (iv), (v), and (vi) will be changed. Because the number of moles of gaseous reactants is greater than the number of moles of gaseous products, the reaction in (iv) will proceed in the forward direction. Because the number of moles of gaseous reactants is smaller than that of gaseous products, the reactions in (i), (iii), (v), and (vi) will shift backward.
Dihydrogen gas is obtained from natural gas by partial oxidation with steam as per following endothermic reaction:
CH4(g)+H2O (g)⇌CO (g)+3H2(g)
a. Write an expression for the above reaction.
Kp=pCO×p^3H2 / pCH4×pH2O
b. How will the values of Kp and composition of equilibrium mixture be affected by
1. Increasing the pressure
Ans: The equilibrium will shift in the backward direction, according to Le Chatelier's principle.
As the reaction shifts in the backward direction as the pressure is increased, the value of Kp decreases.
2. Increasing the temperature
Ans: Because the reaction is endothermic, the equilibrium will shift forward, according to Le Chatelier's principle.
The value of Kp will grow as the temperature rises because the reaction will shift forward.
3. Using a catalyst?
Ans: The existence of a catalyst has no effect on the reaction's equilibrium. A catalyst does nothing but speed up a reaction. As a result, equilibrium will be soon achieved. Because the catalyst only changes the rate of reaction, the value of Kp is unaffected.
Describe the effect of the following on the equilibrium of the reaction:
2H2(g)+CO (g)⇌CH3OH (g)
a. Addition of H2
Ans: According to Le Chatelier's principle, when H2 is added to a reaction, the equilibrium shifts in the forward direction.
b. Addition of CH3OH
Ans: The equilibrium will shift backwards with the addition of CH3OH .
c. Removal of CO
Ans: When CO is removed from the equation, the equilibrium shifts backward.
d. Removal of CH3OH
Ans: When CH3OH is removed from the equation, the equilibrium shifts forward.
At 473 K, equilibrium constant Kr for decomposition of phosphorus pentachloride, PCl5 is 8.3×10−3 . If decomposition is depicted as:
PCl5(g)⇌PCl3(g)+Cl2(g) , ΔrH∘=124.0kJmol−1
a. Write an expression for Kc for the reaction.
Ans: The expression for Kc will be:
Kc=[PCl3] [Cl2] / [PCl5]
b. What is the value of Kc for the reverse reaction at the same temperature?
Ans: Value of Kc for the reverse reaction at the same temperature is:
Kcprime=1 / Kc
=18.3×10^−3=1.2048×10^2
=120−48
c. What would be the effect on Kc if
-
More PCl5 is added?
Ans: Because the temperature is constant in this scenario, Kc will remain constant.
-
Pressure is increased?
Ans: At constant temperature, Kc remains constant. As a result, Kc would not alter in this scenario.
-
The temperature has increased?
Ans: In an endothermic process, the value of Kc rises as the temperature rises. Because the reaction is an endothermic reaction, the value of Kc will rise as the temperature rises.
![]()

Dihydrogen gas used in Haber’s process is produced by reacting methane from natural gas with high temperature steam. The first stage of two stage reaction involves the formation of CO and H2 . In second stage,
CO formed in first stage is reacted with more steam in water gas shift reaction:
CO (g)+H2O (g)⇌CO2(g)+H2(g) If a reaction vessel at 400°C is charged with an equimolar mixture of CO and steam such that pCO=pH2O=4.0 bar , what will be the partial pressure of H2 at equilibrium?
Kp=10.1 at 400°C.
Let the partial pressure of both carbon dioxide and hydrogen gas be p. The given reaction is:
CO (g)+H2O (g)⇌CO2(g)+H2(g)
At equilibrium the concentration of CO and H2O will b (4.0−p).
It is given that, Kp=10.1
Now,
Pco2×p2 / pco×pH2o=Kp
⇒p×p / (4.0−p)(4.0−p)
⇒p40−p=3.178
⇒p=12.712−3.178p
⇒4.178p=12.712
⇒p=3.04
Hence, at equilibrium, the partial pressure of H2 will be 3.04 bar.
Predict which of the following reaction will have appreciable concentration of reactants and products:
-
Cl2(g)⇌2Cl (g) ; Kc=5×10−39
-
Cl2(g)+2NO (g)⇌2NOCl (g) ; Kc=3.7×108
-
Cl2(g)+2NO2(g)⇌2NO2Cl (g) ;Kc=1.8
If the value of Kc lies between 10^−3 and
10^3, a reaction has appreciable concentration of reactants and products. Thus, the reaction given in (c) will have appreciable concentration of reactants and products.
The value of Kc for the reaction 3O2(g)⇌2O3(g) is 2.0×10−50 at 25°C. If the equilibrium concentration of O2 in air at 25°C is 1.6×10^−2 , what is the concentration of O3 ?
The given reaction is:
The reaction CO (g)+3H2(g)⇌CH4(g)+H2O(g) is at equilibrium at 1300 K in a 1L flask. It also contain 0.30 mol of CO , 0.10 mol of H2 and 0.02 mol of
H2O and an unknown amount of CH4 in the flask. Determine the concentration of CH4 in the mixture. The equilibrium constant, Kc for the reaction at the given temperature is 3.90.
Let the concentration of methane at equilibrium be x.
CO (g)+3H2(g)⇌CH4(g)+H2O(g)
At equilibrium, the concentration of CO is 0.3 M , H2 is 0.1 M and
H2O is 0.02 M
What is meant by the conjugate acid-base pair? Find the conjugate acid/base for the following species:
HNO2,CN−,HClO4,F−,OH−,CO32−,S−
A conjugate acid-base pair varies from one other by only one proton. In the table below, the conjugate acid-base for each species is listed.
|
Species |
Conjugate Acid-Base |
|
HNO2 |
NO3− (base) |
|
CN− |
HCN (acid) |
|
HClO4 |
ClO4− (base) |
|
F− |
HF (acid) |
|
OH− |
H2O (acid) / O2− (base) |
|
CO^2 3− |
HCO3− (acid) |
|
S− |
HS− (acid) |
Which of the followings are Lewis acids?
H2O, BF3, H + , NH4+.
Lewis acids are those acids which can accept a pair of electrons. For example:
BF3, H + , NH4 + are Lewis acids.
What will be the conjugate bases for the Brönsted acids:
HF, H2SO4, HCO3
The table below lists the conjugate bases for the given Bronsted acids:
|
Bronsted Acid |
Conjugate Base |
|
HF |
F− |
|
H2SO4 |
HSO4− |
|
HCO3− |
CO^2 3− |
Write the conjugate acids for the following Brönsted bases:
NH2−,NH3,HCOO−
The table below lists the conjugate acids for the given Bronsted bases:
|
Bronsted Base |
Conjugate Acid |
|
NH2− |
NH3 |
|
NH3 |
NH4− |
|
HCOO− |
HCOOH |


The species:
H2O,HCO3−,HSO4−,NH3 can act both as Brönsted acids and bases. For each case give the corresponding conjugate acid and base.
The table below lists the conjugate acids and conjugate bases for the given species.
|
Species |
Conjugate Acid |
Conjugate Base |
|
H2O |
H3O + |
OH |
|
HCO3− |
H2CO3 |
CO32− |
|
HSO4− |
H2SO4 |
SO42− |
|
NH3 |
NH4 + |
NH2− |
Classify the following species into Lewis acids and Lewis bases and show how these act as Lewis acid/base:
a. OH−
Ans: OH−is a Lewis base since it can donate its lone pair of electrons
b. F−
Ans: F− is a Lewis base since it can donate a pair of electrons.
c. H +
Ans: H + is a Lewis acid since it can accept a pair of electrons.
d. BCl3
Ans: BCl3 is a Lewis acid since it can accept a pair of electrons.
The concentration of hydrogen ion in a sample of soft drink is 3.8×10−3 M . what is its pH?
Given, [H + ]=3.8×10−3 M
Therefore, the pH value of the soft drink:
pH=−log[H+]
pH=−log(3.8×10−3)
pH=−log3.8−log10−3
pH=−log3.8+3
pH=−0.58+3
pH=2.42
The pH of a sample of vinegar is 3.76. Calculate the concentration of hydrogen ion in it.
Given the, pH=3.76
It is known as:
pH=−log[H+]
log[H+]=−pH
[H+]=antilog(−pH)
[H+]=antilog(−3.76)
[H+]=1.74×10−4M
Hence, the concentration of hydrogen ion in the given sample of vinegar is 1.74×10−4 M.
The ionization constant of HF, HCOOH, HCN at 298 K are 6.8×10−4 , 1.8×10−4 and 4.8×10−9 respectively. Calculate the ionization constants of the corresponding conjugate base.
It is known as:
Kb=KwKa
Given,
Ka of HF is 6.8×10−4
Hence,Kb of its conjugate base
Kb=KwKa
Kb=10−146.8×10−4
Kb=1.5×10−11
Given Ka of HCOOH is
10^−4
Hence, Kb of its conjugate base
The ionization constant of phenol is 1.0×10−10 . What is the concentration of phenolate ion in 0.05 M Ans:of phenol? What will be its degree of ionization if the Ans:is also 0.01M in sodium phenolate?
According to the reaction of ionization of phenol:
C6H5OH+H2O⇌C6H5O−+H3O+
The initial concentration of C6H5OH is 0.05 M.
At equilibrium, the concentration of C6H5O− and H3O+ will be x, then the concentration of C6H5OH will be (0.05−x).
The first ionization constant of 9.1×10−8 . Calculate the concentration of HS− ion in its 0.1 M solution. How will this concentration be affected if the Ans:is 0.1 M in HCl also? If the second dissociation constant of H2S is 1.2×10−13 , calculate the concentration of S2− under both conditions.
To calculate the concentration of HS− ion:
Case I (in the absence of HCl ):
Let the concentration of HS−be x M:
H2S⇌H + +HS−
The final concentration of H2S will be (0.1−x)
Then,
Kai=[H+][HS−] / [H2S]
9.1×10^−8 = (x)(x) / 0.1−x
(9.1×10−8)(0.1−x)=x2
Taking, 0.1−xM;0.1M we have (9.1×10−8)(0.1) = x^2
9.1×10−9=x^2
x = √9.1×10−9
=9.54×10−5M
⇒[HS−]=9.54×10−5M
Case II (in the presence of HCl):
In the presence of 0.1 M of HCl, let [HS−] be y M.
H2S⇌H + +HS−
The final concentration of H2S will be (0.1−y)
Now,
Ka1= [HS−][H+] / [H2S]
Ka1=y(0.1+y)(0.1−y)
=9.1×10−8 = y×0.10.1
y=9.1×10−8
The concentration of [HS−]=9.1×10−8
To calculate the concentration of [S2−]
Case I (in the absence of 0.1 M of HCl):
HS−⇌H++S2−
[HS−]=9.54×10−5 M
Let [S2−] be X .
Also,
[H+]=9.54×10^−5 M
Ka2=[H+][S2−] / [HS−]
Ka2=(9.54×10^−5)(X) / 9.54×10−5
1.2×10−13=X=[S2−]
Case II (in the presence of 0.1 M of HCl):
The concentration of S2− be X' M
[HS−]=9.1×10−8 M
[H+]=0.1 M
Then,
Ka2=[H+][S2] / [HS−]
1.2×10−13=(0.1)(X′) / 9.1×10−8
10.92×10−21=0.1X′
10.92×10−210.1=X′
X′=1.092×10−200.1
=1.092×10−19M
⇒Ka1=1.74×10−5
The ionization constant of acetic acid is 1.74×10−5 . Calculate the degree of dissociation of acetic acid in its 0.05 M solution. Calculate the concentration of acetate ion and its pH.
For the reaction:
CH3COOH+H2O⇌CH3COO−+H3O+
The final concentration of H3O + is 0.05α . Then the final concentration of CH3COOH will be (0.05−0.05α) .
Ka=(.05α)(.05α) / (.05−0.05α)
=(.05α)(0.05α) / .05(1−α)
=.05α^2 / 1−α
1.74×10^−5=.05α^2 / 1−α
1.74×10^−5−1.74×10^−5α=0.05α^2
0.05α^2+1.74×10^−5α−1.74×10^−5
D=b2−4ac
=(1.74×10−5)2−4(.05)(1.74×10−5)
=3.02×10−25+.348×10−5
α = √K / ac
α= √ 1.74×10^−5.05
= √ 34.8×10^−5×10 / 10
√=3.48×10^−6
[CH3COO−]=0.05×1.86×10−3
=0.93×10^−3 / 1000
=.000093
pH=−log[H+]
=−log(.093×10−2)
∴pH=3.03
Hence, the concentration of acetate ion in the Ans:is 0.00093 M and its pH is 3.03.
It has been found that the pH of 0.01M of an organic acid is 4.15. Calculate the concentration of the anion, the ionization constant of the acid and its pKa .
Let the organic compound be
Assuming complete dissociation, calculate the pH of the following solutions:
a. 0.003 M HCl
Ans:
H2O+HCl⇌H3O++Cl−
Since HCl is completely ionized.
[H3O+]=[HCl]⇒[H3O+]=0.003
pH=−log[H3O+]
pH=−log(0.003)
pH=2.52
Hence, the pH of the solution is 2.52.
b. 0.005 M NaOH
Ans:
NaOH(aq)⇌Na+(aq)+OH−(aq)
[OH−]=[NaOH]⇒[OH−]=0.005
pOH=−log[OH−]
pOH=−log(0.005)
pOH=2.30
pH=14−pOH
pH=14−2.30
pH=11.70
Hence, the pH of the solution is 11.70.
c. 0.002 M HBr
Ans:
HBr+H2O⇌H3O++Br−
[H3O+]=[HBr]⇒[H3O+]=0.002
pH=−log[H3O+]
pH=−log(0.002)
pH=2.69
Hence, the pH of the solution is 2.69.
d. 0.002 M KOH
Ans:
KOH(aq)⇌K+(aq)+OH−(aq)
[OH−]=[KOH]
⇒[OH−]=0.002
pOH=−log[OH−]
pOH=−log(0.002)
pOH=2.69
pH=14−pOH
pH=14−2.69
pH=11.31
Hence, the pH of the solution is 11.31.
Calculate the pH of the following solutions:
a. 2 g of TlOH dissolved in water to give 2 litre of solution.
The degree of ionization of a 0.1M bromoacetic acid is 0.132. Calculate the pH of pKa of bromoacetic acid.
Degree of ionization,
α=0.132
Concentration, c = 0.1 M
Thus, the concentration of
[H3O+] = 0.1×0.132
[H3O+]=0.0132
pH=−log[H+]
pH=−log(0.0132)
pH=1.88
Now,
Ka=Cα2
Ka=0.1×(0.132)2
Ka=0.0017p
Ka=2.75
What is the pH of 0.001 M aniline solution? The ionization constant of aniline can be taken from Table 7.7. Calculate the degree of ionization of aniline in the solution. Also calculate the ionization constant of the conjugate acid of aniline.
The degree of ionization of a 0.1M bromoacetic acid is 0.132. Calculate the pH and the pKa of bromoacetic acid.
Ans: Degree of ionization,
α=0.132
Concentration,
c=0.1M
Thus, the concentration of
⇒0.1×0.132=0.0132
pH=−log[H+]=−log(0.0132)=1.879:1.88
Now
Cα2 = 0.1×(0.132)^2
Ka=.0017p
Ka=2.75
What is the pH of 0.001M aniline solution? The ionization constant of aniline can be taken from Table 7.7. Calculate the degree of ionization of aniline in the solution. Also calculate the ionization constant of the conjugate acid of aniline.
Calculate the degree of ionization of 0.05M acetic acid if its pKa value is 4.74. How is the degree of dissociation affected when it's also contains
a. 0.01M
b. 0.1 M in HCL
Calculate the hydrogen ion concentration in the following biological fluids whose pH are given below:
a. Human muscle fluid 6.83
pH=6.83pH=−log[pH=6.83pH=−log[H+]
∴6.83=−log[H+]
[H+]=1.4810−7M
b. Human stomach fluid, 1.2:
pH=1.2 × 1.2=−log[H+]
∴[H+]=0.063
c. Human blood, 7.38:
pH=7.38=−log[H+]
∴[H+]=4.1710−8M
d. Human saliva, 6.4:
pH=6.4× 6.4=−log[H+]
[H+]=3.9810−7
The pH of milk, black coffee, tomato juice, lemon juice and egg white are
6.8,5.0,4.2,2.2 and 7.8 respectively. Calculate corresponding hydrogen ion concentration in each.
The hydrogen ion concentration in the given substances can be calculated by using the given relation:
pH=−log[H+]
1. pH of milk = 6.8
Since,pH=−log[H+]
6.8=−log[H+]log
[H+]=−6.8 =anitlog(−6.8)
[H+]=anitlog(−6.8)
=1.519−7M
2. pH of black coffee = 5.0
Since,
pH=×log[H+]
5.0=−log[H+]log
[H+]=−5.0
[H+]=anitlog(−5.0)
=10−5M
3. pH of tomato juice = 4.2
Since,
pH=−log[H+]
4.2=−log[H+]log
[H+]=−4.2
[H+]=anitlog(−4.2)
=6.3110−5M
4. pH of lemon juice = 2.2
Since,
pH=− log
2.2=−log[H+]log
[H+]=−2.2
[H+]=anitlog(−2.2)
=6.3110−3M
5. pH of egg white = 7.8
Since,
pH=−log[H+]
7.8=−log[H+]log
[H+]=−7.8
[H+]=anitlog(−7.8)
=1.5810−8M
If 0.561g of KOH is dissolved in water to give 200mL at 298K. Calculate the concentrations of potassium, hydrogen and hydroxyl ions. What is its pH ?
[KOHaq]=0.56115g/L
=2.805g/L
=2.805×156.11M=.05M
KOHaq→K(aq)++OH(aq)−
[OH−]=.05M
=[K+][H+][H−]=Kw
[H+]=Kw[OH−]
=10−140.05
=2×10−11M
∴pH=12.70
The solubility of Sr(OH)2 at 298K is 19.23g/L of solution. Calculate the concentrations of strontium and hydroxyl ions and the pH of the solution.
Solubility of Sr(OH)2=19.23g/L
Then, concentration of Sr(OH)2 =19.23121.63M
=0.1581M
Sr(OH)2(aq)→Sr(aq)2++2(OH−)(aq)
∴[Sr2+]=0.1581M
[OH−]=2×0.1581M=0.3126M
Now,
Kw=[OH−][H+]
10−140.3126=[H+]
⇒[H+]=3.2×10−14
∴pH=13.495;13.50
The ionization constant of propanoic acid is 1.32×10−5. Calculate the degree of ionization of the acid in its 0.05M Ans:and also its pH. What will be its degree of ionization if the Ans:is 0.01M in HCl also?
Let the degree of ionization of propanoic acid be α. Then, representing propionic acid as HA, we have:
HA +H2O⇔H3O+ + A−
(.05−0.0α)≈0.5.05α / .05^α
=(.05α)(.05α) / 0.05=.05α^2
α=Ka.05=1.63×10^−2
Then,
[H3O+]=.05α=.05×1.63×10−2=Kb.15×10^−4M
∴pH=3.09
In the presence of 0.1M of HCl, let α ' be the degree of ionization.Then,
[H3O+]=0.01
[A−]=005α′
[HA]=.05
Ka=0.01×.05α′.05
′1.32×10−5=.01×α′
α′=1.32×10^−5
The pH of 0.1M of cyanic acid (HCNO) is 2.34. Calculate the ionization constant of the acid and its degree of ionization in the solution.
c=0.1M
pH=2.34
−log[H+]=pH
−log[H+]=2.34
[H+]=4.5×10^−3
Also,
[H+]=cα
4.5×10−30.1=α
α=4.5×10^−3=.045 Then,
=0.1×(45×10−3)^2
=202.5×10^−6
=2.02×10^−4
The ionization constant of nitrous acid is 4.510^−4. Calculate the pH of
0.04M sodium nitrite and also its degree of hydrolysis.
A 0.02M solution of pyridinium hydrochloride has pH=3.44. Calculate the ionization constant of pyridine
pH=3.44
We know that,
pH=−log[H+]
∴[H+]=3.63×10−4
Then,
Kb=(3.63×10−4)20.02(∵ concentration =0.02M)
⇒Kb=6.6×10−6
Now,
Kb=KwKa
⇒Ka=Kw / Ka = 10^−14 / 6.6×10^−6 = 1.51×10^−9
Predict if the solutions of the following salts are neutral, acidic or basic:
NaCl,KBr,NaCN,NH4NO3,NaNO2 and KF
(i) NaCl :
NaCl+H2O↔NaOH+HCl
Strong base Strong base
Therefore, it is a neutral solution.
(ii) KBr:
KBr+H2O↔KOH+HBr
Strong base Strong base
Therefore, it is a neutral solution.
iii) NaCN:
NaCN+H2O↔HCN+NaOH
Weak acid Strong base
Therefore, it is a basic solution.
(iv) NH4NO3
NH4NO3+H2O↔NH4OH+HNO3
Weak acid Strong base
Therefore, it is an acidic solution.
(v) NaNO2
NaNO2+H2O↔NaOH+HNO2
Strong base Weak acid
Therefore, it is a basic solution.
(vi) KF
KF+H2O↔KOH+HF
Strong base Weak acid
Therefore, it is a basic solution.
The ionization constant of chloro acetic acid is 1.3510−3. What will be the
pH of 0.1M acid and its 0.1M sodium salt solution?

Calculate the pH of the resultant mixtures:
a. 10mL of 0.2MCa(OH)2+25mL of 0.1MHCl
Ans: Moles of
H3O+=25×0.1 / 1000=.0025mol
OH−=10×0.2×2 / 1000=.0040mol
Thus, excess of OH−=.0015mol
b. 10mL of 0.01MH2SO4+10mL of 0.01MCa(OH)2
Ans: Moles of H3O+=2×10×0.1 / 1000=.0002mol
Moles of OH−=2×10×0.1 / 1000=.0002mol
Since there is neither an excess of The solution is neutral. Hence, pH=7.
c. 10mL of 0.1MH2SO4+10mL of 0.1MKOH
Ans: Moles of H3O+=2×10×0.11000=.002mol
Moles of OH−=10×0.11000=0.001mol
Excess of H3O+=.001mol
Thus,
[H3O+]=.00120×10−3=10−320×10−3=.05
∴pH=−log(0.05)
∴pH=−log(0.05)
=1.30
=1.30
Determine the solubility of silver chromate, barium chromate, ferric hydroxide, lead chloride and mercuric iodide at 298K from their solubility product constants given in Table 7.9 (page 221). Determine also the molarities of individual ions.
1. Silver chromate: Ag2CrO4→2Ag++CrO42−
Then,
Ksp=[Ag+]2[CrO42−]
Let the solubility of Ag2CrO4 be
⇒[Ag+]=2s and [CrO42−]=s
Then,
Ksp=(2s)2⋅s=4s3
⇒1.1×10−12=4s3
.275×10−12=s3
MolarityofAg+=2s=2x0.65x10^−4=1.30x10^−4M
Molarity of CrO42−=s=0.65×10^−4M
2. Barium Chromate:
BaCrO4→Ba2++CrO42−
Then,
Ksp=[Ba2+][CrO42−]
Let the solubility of BaCrO4 be [Ba2+]=s and [CrO42−]=s⇒Ksp=s2
⇒1.2×10−10=s2
M ⇒s=1.09×10^−5M
Molarity of Ba2+= Molarity of
CrO42−=s=1.09×10−5M
3. Ferric Hydroxide:
Fe(OH)3→Fe2+3OH−
Ksp=[Fe2+][OH−]3
Let s be the solubility of Fe(OH)3
Molarity of OH−=3s=4.17×1010M
4. Lead Chloride:
PbCl2→Pb2++2Cl−
KSP=[Pb2+][Cl−]2
KSP be the solubility of
[PB2+]=s and [Cl−]=2s
Thus, Ksp=s.(2s)2
⇒1.6×10−5=4s3
⇒0.4×10−5=s3
4×10−6=s3⇒1.58×10−2M=S.1
Molarity of chloride
=2s=3.16×10−2M
5. Mercurous Iodide:
Hg2I2→Hg2++2I−
Ksp=[Hg22+][I−]2
Let s be the solubility of
⇒[Hg22+]=s and [I−]=2s
Thus,
Ksp=s(2s)2⇒Ksp=4s3
4.5×10−29=4s3
1.125×10−29=s3
⇒s=2.24×10−10M
Molarity of Hg22+=s=2.24×10−10M
Molarity of I−=2s=4.48×10−10M
The solubility product constant of Ag2CrO4 and AgBr are 1.1×10−12 and 5.0×1013 respectively. Calculate the ratio of the molarities of their saturated solutions.
Let s be the solubility of Ag2CrO4
Then, Ag2CrO4→Ag2++2CrO42−
Ksp=(2s)2⋅s=4s3
1.1×10^−12=4s3
s=6.5×10^−5M
Let s′ be the solubility of AgBr.
AgBr(s)↔Ag++Br−
Ksp=s′2=5.0×10^−13
∴s′=7.07×10^−7M
Therefore, the ratio of the molarities of their saturated solution is
ss′=6.5×10^−5M / 7.07×10^−7M = 91.9
Equal volumes of 0.002M solutions of sodium iodate and cupric chlorate are mixed together. Will it lead to precipitation of copper iodate?
(For cupric iodate Ksp=7.4×10−8)
When equal volumes of sodium iodate and cupric chlorate solutions are mixed together, then the molar concentrations of both solutions are reduced to half i.e. 0.001M. Then,
NalO3→Na++lO3− 0.001M0.001M
Cu(ClO3)2→Cu2++2ClO3−
0.001M0.001M
0.001M0.001M
Now, the solubility equilibrium for copper iodate can be written as:
Cu(lO3)2→Cu(aq)2++2lO3(aq)−
Ionic product of copper iodate:
=[Cu2+]×[lO3−]2
=(0.001)(0.001)2
=1×10−9
Since the ionic product (1×10−9) is less than (7.4×10−8), precipitation will not occur.
The ionization constant of benzoic acid is 6.46×10−5 and Ksp for silver benzoate is 2.5×10−13. How many times is silver benzoate more soluble in a buffer of pH=3.19 compared to its solubility in pure water?
What is the maximum concentration of equimolar solutions of ferrous sulphate and sodium sulphide so that when mixed in equal volumes, there is no precipitation of iron sulphide?
(For iron sulphide, Ksp=6.310−18)
Let the maximum concentration of each solution be xmol/L. After mixing, the volume of the concentrations of each solution will be reduced to half i.e. x/2.
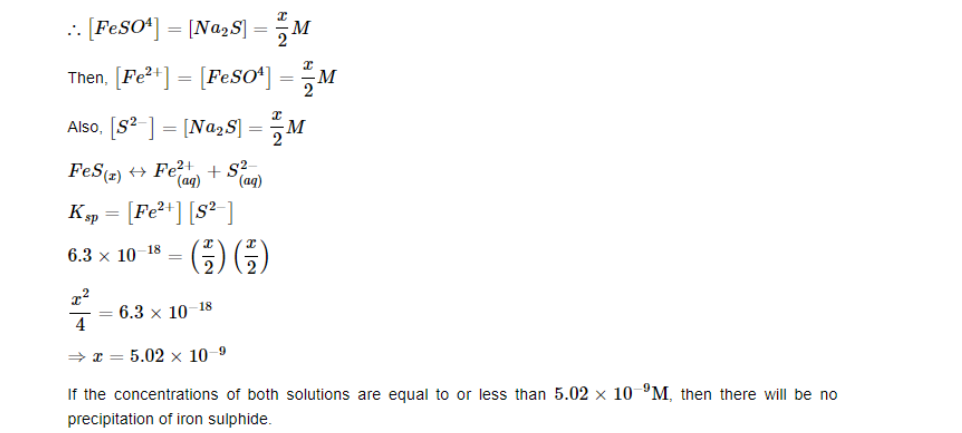

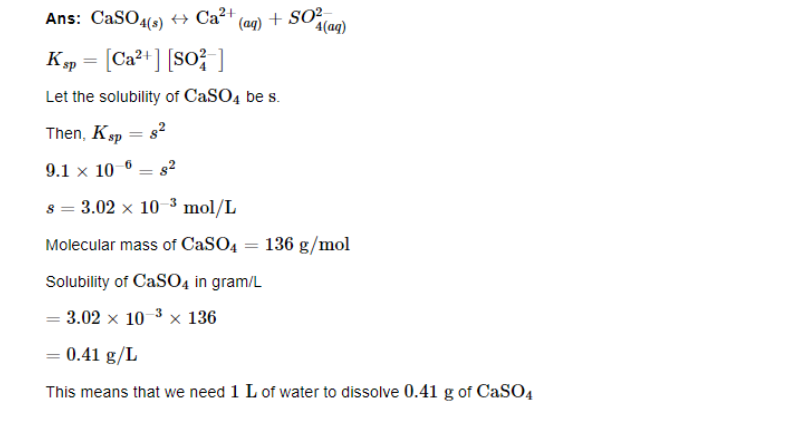
If the concentrations of both solutions are equal to or less than 5.02×10^−9M, then there will be no precipitation of iron sulphide.
What is the minimum volume of water required to dissolve 1g of calcium sulphate at 298 K? (For calcium sulphate, Ksp is 9.1 10^−6)
CaSO4(s)↔Ca2+(aq)+SO4(aq)2−
Ksp=[Ca2+][SO42−]
Let the solubility of CaSO4 be s.
Then,
Ksp=s^2
9.1×10−6=s2
s=3.02×10−3mol/L
Molecular mass of CaSO4=136g/mol
Solubility of CaSO4 in gram/L =3.02×10−3×136
=0.41g/L
This means that we need 1L of water to dissolve 0.41g of CaSO4
Therefore, to dissolve 1g of CaSO4 we require
=1 / 0.41L=2.44L of water.
Admissions Open for 2025-26

