In Chapter 3 of Class 9 Maths, "Coordinate Geometry," students will get into a world of geometric concepts and their representation in a coordinate plane. Our NCERT solutions carefully break down the chapter and provide step-by-step elucidation for a proper understanding of coordinate geometry and its applications.
Students can access the NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry. Curated by experts according to the CBSE syllabus for 2025–2026, these step-by-step solutions make Maths much easier to understand and learn for the students. These solutions can be used in practice by students to attain skills in solving problems, reinforce important learning objectives, and be well-prepared for tests.
How will you describe the position of a table lamp on your study table to another person?
To describe the position of a table lamp placed on the table, let us consider the table lamp as P and the table as a plane.
Now choose two perpendicular edges of the table as the axes OX and OY.
Measure the perpendicular distance ‘a’cm of P (lamp) from OY. Measure the perpendicular distance ‘b’ cm of P (lamp) from OX.
Thus, the position of the table lamp P is described by the ordered pair (a, b).
(Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction. All other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1 cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.
There are many cross-streets in your model. A particular cross-street is made by two streets, one running in the North-South direction and another in the East-West direction. Each cross street is referred to in the following manner: If the 2nd street running in the North-South direction and 5th in the East-West direction meet at some crossing, then we will call this cross-street (2,5). Using this convention, find:
(i) how many cross-streets can be referred to as (4,3).
(ii) how many cross-streets can be referred to as (3,4).
(i) A unique cross street as shown by the point A(4, 3).
(ii) A unique cross street as shown by the point B(3,4).
The two cross streets are uniquely found because of the two reference lines we have used for locating them.
.png)
Write the answer of each of the following questions:,
(i) What is the name of horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?
(ii) What is the name of each part of the plane formed by these two lines?
(iii) Write the name of the point where these two lines intersect.
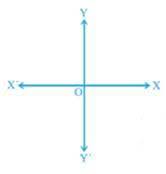
(i) The horizontal line that is drawn to determine the position of any point in the Cartesian plane is called as x-axis.
The vertical line that is drawn to determine the position of any point in the Cartesian plane is called as y-axis.
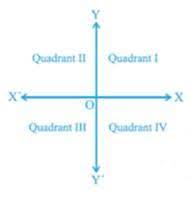
(ii) The name of each part of the plane that is formed by x-axis and y-axis is called as quadrant.
(iii) The point, where the x-axis and the y-axis intersect is called as origin.
See Fig.3.14, and write the following :
(i) The coordinates of B.
(ii)The coordinates of C.
(iii)The point identified by the coordinates (–3, –5).
(iv) The point identified by the coordinates (2, – 4).
(v) The abscissa of the point D.
(vi) The ordinate of the point H.
(vii) The coordinates of the point L.
(viii) The coordinates of the point M.
.png)
We need to consider the given below figure to answer the following questions.
(i) The coordinates of point B in the above figure is the distance of point B from x-axis and y-axis. Therefore, we can conclude that the coordinates of point B are (―5, 2).
(ii) The coordinates of point C in the above figure is the distance of point C from x-axis and y-axis. Therefore, we can conclude that the coordinates of point C are (5, ―5).
(iii) The point that represents the coordinates (―3, ―5) is E.
(iv) The point that represents the coordinates (2, ―4) is G.
(v) The abscissa of point D in the above figure is the distance of point D from the y-axis. Therefore, we can conclude that the abscissa of point D is 6.
(vi) The ordinate of point H in the above figure is the distance of point H from the x-axis. Therefore, we can conclude that the abscissa of point H is ―3.
(vii) The coordinates of point L in the above figure is the distance of point L from x-axis and y-axis. Therefore, we can conclude that the coordinates of point L are (0, 5).
(viii) The coordinates of point M in the above figure is the distance of point M from x-axis and y-axis. Therefore, we can conclude that the coordinates of point M are (―3, 0).
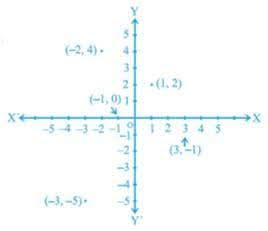
In which quadrant or on which axis do each of the points (- 2, 4), (3, – 1), (- 1, 0), (1, 2) and (- 3, – 5) lie? Verify your answer by locating them on the Cartesian plane.
We need to determine the quadrant or axis of the points (– 2, 4), (3, – 1), (- 1, 0), (1, 2) and (– 3, – 5).
First, we need to plot the points (– 2, 4), (3, – 1), (- 1, 0), (1, 2) and (– 3, – 5) on the graph, to get
We need to determine the quadrant, in which the points (– 2, 4), (3, – 1), (- 1, 0), (1, 2) and (– 3, – 5) lie.
From the figure, we can conclude that the point (– 2, 4) lie in IInd quadrant.
From the figure, we can conclude that the point (3, – 1) lie in IVth quadrant.
From the figure, we can conclude that the point (–1, 0) lie on x-axis.
From the figure, we can conclude that the point (1, 2) lie in Ist quadrant.
From the figure, we can conclude that the point (– 3, – 5) lie in IIIrd quadran
Plot the point (x, y) given in the following table on the plane, choosing suitable units of distance on the axis.
|
x |
− 2 |
− 1 |
0 |
1 |
3 |
|
y |
8 |
7 |
−1.25 |
3 |
− 1 |
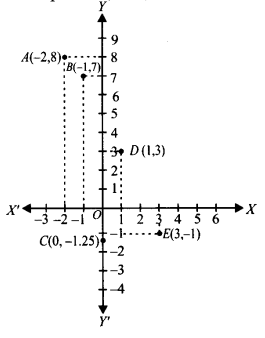
The given points are (-2, 8), (-1, 7), (0, -1.25), (1,3) and (3, -1).
To plot these points:
(i) We draw X’OX and YOY’ as axes.
(ii) We choose suitable units of distance on the axes.
(iii) To plot (-2,8), we start from O, take (-2) units on x-axis and then (+8) units on y – axis. We mark the point as A (-2, 8).
(iv) To plot (-1,7), we start from O, take (-1) units on x-axis and then (+7) units on the y – axis. We mark the point as B(-1, 7).
(v) To plot (0, -1.25), we move along 1.25 units below the x-axis on the y – axis and mark the point as C(0, -1.25).
(vi) To plot (1, 3), we take (+1) unit on the x-axis and then (+3) units on the y – axis. We mark the point as D(1, 3).
(vii) To plot (3, -1), we take (+3) units on the x-axis and then (-1) unit on the y – axis. We mark the point E(3, -1).
