NCERT Solutions for Class 10 Maths Chapter 7: Coordinate Geometry

(i) Distance between the points is given by

Therefore the distance between (2,3) and (4,1) is given by

l =

=

= √4+4 = √8 = 2√2

(ii)Applying Distance Formula to find distance between points (–5, 7) and (–1, 3), we get

l =

 =

 = √16+16 = √32 = 4√2

(iii)Applying Distance Formula to find distance between points (a, b) and (–a, –b), we get

l =

=

=

 

Applying Distance Formula to find distance between points (0, 0) and (36, 15), we get

=

= √1296 + 225 = √1521 = 39

Yes, we can find the distance between the given towns A and B.

Assume town A at origin point (0, 0).

Therefore, town B will be at point (36, 15) with respect to town A.

And hence, as calculated above, the distance between town A and B will be 39km

 

Let A = (1, 5), B = (2, 3) and C = (–2, –11)

Using Distance Formula to find distance AB, BC and CA.

BC =

CA =

Since AB+BC ≠ CA

Therefore, the points (1, 5), (2, 3), and (−2, −11) are not collinear.

 

Using Distance formula, we have

⇒

⇒ 64 + (y +3)² = 100

⇒ (y+3)² = 100-64 = 36

⇒ y+3 = ± 6

⇒ y+3=6 or y+3 = - 6

Therefore y = 3 or -9

 

Let A = (5, –2), B = (6, 4) and C = (7, –2)

Using Distance Formula to find distances AB, BC and CA.

AB =

BC =

CA =

Since AB = BC.

Therefore, A, B and C are vertices of an isosceles triangle.

 

We have A = (3, 4), B = (6, 7), C = (9, 4) and D = (6, 1)

Using Distance Formula to find distances AB, BC, CD and DA, we get

AB =

BC =

CD =

AD =

Therefore, All the sides of ABCD are equal here

Now, we will check the length of its diagonals.

AC =

BD =

So, Diagonals of ABCD are also equal.

we can definitely say that ABCD is a square.

Therefore, Champa is correct.

 

(i)Let A = (–1, –2), B = (1, 0), C= (–1, 2) and D = (–3, 0)

Using Distance Formula to find distances AB, BC, CD and DA, we get

AB =

BC =

CD =

AD =

Therefore, all four sides of quadrilateral are equal.

Now, we will check the length of diagonals.

AC =

BD =

Therefore, diagonals of quadrilateral ABCD are also equal.

we can say that ABCD is a square.

(ii)Let A = (–3, 5), B= (3, 1), C= (0, 3) and D= (–1, –4)

Using Distance Formula to find distances AB, BC, CD and DA, we get

AB =

BC =

CD =

DA =

We cannot find any relation between the lengths of different sides.

Therefore, we cannot give any name to the quadrilateral ABCD.

(iii)Let A = (4, 5), B= (7, 6), C= (4, 3) and D= (1, 2)

Using Distance Formula to find distances AB, BC, CD and DA, we get

AB =

BC =

CD =

DA =

Here opposite sides of quadrilateral ABCD are equal.

We can now find out the lengths of diagonals.

AC =

BD =

Here diagonals of ABCD are not equal.

 we can say that ABCD is not a rectangle therefore it is a parallelogram.

Let the point be (x, 0) on x–axis which is equidistant from (2, –5) and (–2, 9).

Using Distance Formula and according to given conditions we have:

⇒

Squaring both sides, we get

⇒

(x-2)² + 25 = (x+2)² + 81

x² + 4 - 4x + 25 = x² + 4 + 4x + 81

8x = - 25 - 81

8x = -56

x = - 7

Therefore, point on the x–axis which is equidistant from (2, –5) and (–2, 9) is (–7, 0)

It is given that Q is equidistant from P and R. Using Distance Formula, we get

PQ = RQ

⇒√25+16 = √x² + 25

⇒41 = x² + 25

 16 = x²

 x = ± 4

Thus, R is (4, 6) or (–4, 6).

When point R is (4,6)

 PR =

 QR =

When point R is (- 4,6)

PR =

 QR =

 

It is given that (x, y) is equidistant from (3, 6) and (–3, 4).

Using Distance formula, we can write

⇒

⇒ (x-3)² + (y-6)² = (x+3)² + (y-4)²

⇒ x² + 9 -6x + y² + 36 - 12y = x² + 9 + 6x + y² + 16 - 8y

⇒36- 16 = 6x + 6x + 12y  - 8y

⇒20 = 12x + 4y

⇒3x + y = 5

⇒3x + y - 5 = 0

 

 

Let P(x, y) be the required point. Using the section formula

Therefore the point is (1,3).

 

 

Let P (x1,y1) and Q (x2,y2) are the points of trisection of the line segment joining the given points i.e., AP = PQ = QB

Therefore, point P divides AB internally in the ratio 1:2.

Therefore P(x1,y1) = (2, -5/3)

Point Q divides AB internally in the ratio 2:1.

Q (x2 ,y2) = (0, -7/3)

 

Let the ratio in which the line segment joining ( -3, 10) and (6, -8) is divided by point ( -1, 6) be k:1.
Therefore, -1 = 6k-3/k+1
-k - 1 = 6k -3
7k = 2
k = 2/7
Therefore, the required ratio is 2:7.

 

Let the ratio in which the line segment joining A (1, - 5) and B ( - 4, 5) is divided by x-axis be k:1.
Therefore, the coordinates of the point of division is (-4k+1/k+1, 5k-5/k+1).

We know that y-coordinate of any point on x-axis is 0.

∴ 5k-5/k+1 = 0

Therefore, x-axis divides it in the ratio 1:1.

To find the coordinates let's substitute the value of k in equation(1)

 

Required point = [(- 4(1) + 1) / (1 + 1), (5(1) - 5) / (1 + 1)]

 

= [(- 4 + 1) / 2, (5 - 5) / 2]

 

= [- 3/2, 0]

 

Let A,B,C and D be the points (1,2) (4,y), (x,6) and (3,5) respectively.

 

Let (x,y) be the coordinate of A.

Since AB is the diameter of the circle, the centre will be the mid-point of AB.

now, as centre is the mid-point of AB.

x-coordinate of centre = (2x+1)/2​

y-coordinate of centre = (2y+4)/2​

But given that centre of circle is (2,−3).

Therefore,

(2x+1)/2​=2⇒x=3

(2y+4​)/2=−3⇒y=−10

Thus the coordinate of A is (3,−10).

 

As given the coordinates of A(−2,−2) and B(2,−4) and P is a point lies on AB.

And AP = 3/7 ​AB

∴BP = 4/7

Then, ratio  of AP and PB = m1​:m2 ​= 3:4

Let the coordinates of P be (x,y).

∴ x = (m1​x2​ + m2​x1) / (m1​ + m2​)​​

⇒ x = (3 × 2 + 4 × (−2)) / (3 + 4) ​ = (6 − 8) / 7 ​= −2 / 7​

And y = (m1​y2​ + m2​y1) / (m1​ + m2​)​​​​

⇒ y = ((3 × (−4) + 4 × (−2)) / (3 + 4) ​= (−12−8) / 7 ​= −20 / 7​

∴ Coordinates of P = −2 / 7​, −20 / 7​

 

From the figure, it can be observed that points X,Y,Z are dividing the line segment in a ratio 1:3,1:1,3:1 respectively.

Using Sectional Formula, we get,

Coordinates of X = ((1 × 2 + 3 × (−2)) / (1 + 3), (1 × 8 + 3 × 2) / (1 + 3))


= (−1, 7/2)

Coordinates of Y = (2 − 2) / 2, (2 + 8) / 2 = (0,5)


Coordinates of Z = ((3 × 2 + 1 × (−2)) / (1 + 3), (3 × 8 + 1 × 2) / (1 + 3)


= (1, 13/2)

Let (3, 0), (4, 5), ( - 1, 4) and ( - 2, - 1) are the vertices A, B, C, D of a rhombus ABCD.

Length of the diagonal AC=


Length of the diagonal BD=

Area of rhombus ABCD = 1/2 X 4√2 X 6√2= 24 square units.
Therefore, the area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2,-1) taken in order, is 24 square units.

 

 

 

(i) (2, 3), (–1, 0), (2, –4)

Area of Triangle is given by

Area of Triangle =

Area of  the given triangle = ½[2 {0 − (−4)} – 1 (−4 − 3) + 2 (3 − 0)]

=½ (8 + 7 + 6) = 21/2 sq. units

(ii) (–5, –1), (3, –5), (5, 2)

Area of the given triangle = ½ [−5 (−5 − 2) + 3 {2 − (−1)} + 5 {−1 − (−5)}]

= ½(35 + 9 + 20)

= 32 sq. units

 

(i) (7, –2), (5, 1), (3, k)

Since, the given points are collinear, it means the area of triangle formed by them is equal to zero.

Therefore, for points (7, -2) (5, 1), and (3,k), area = 0

⇒ ½[7 (1 − k) + 5 {k − (−2)} + 3 (−2 − 1)]

= ½(7 − 7k + 5k + 10 − 9) = 0

⇒ ½(7 − 7k + 5k + 1) = 0

⇒ ½(8 − 2k) = 0

⇒ 8 − 2k = 0

⇒ 2k = 8

⇒ k = 4

(ii) (8, 1), (k, –4), (2, –5)

Since, the given points are collinear, it means the area of triangle formed by them is equal to zero.

Therefore, for points (8, 1) (k, -4), and (2,-5), area = 0

⇒ ½[8 {−4 − (−5)} + k (−5 − 1) + 2 {1 − (−4)}]

= ½(8 − 6k + 10) = 0

⇒ ½(18 − 6k) = 0

⇒18 − 6k = 0

⇒ 18 = 6k

⇒ k = 3

Let the vertices of the triangle be A (0, -1), B (2, 1), C (0, 3).

Let D, E, F be the mid-points of the sides of this triangle. Coordinates of D, E, and F are given by

D = (0+2/2 , -1+1/2) = (1,0)

E = (0+0/2 , -3-1/2) = (0,1)

Area of a triangle = 1/2 {x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2)}

Area of ΔDEF = 1/2 {1(2-1) + 1(1-0) + 0(0-2)}

                     = 1/2 (1+1) = 1 square units

Area of ΔABC = 1/2 [0(1-3) + 2{3-(-1)} + 0(-1-1)]

                      = 1/2 {8} = 4 square units

Therefore, the required ratio is 1:4.

 

Let the vertices of the quadrilateral be A ( - 4, - 2), B ( - 3, - 5), C (3, - 2), and D (2, 3). Join AC to form two triangles ΔABC and ΔACD.

Area of a triangle = 1/2 {x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2)}

Area of ΔABC =1/2[−4 (−5 − 2) – 3 {-2 − (−2)} + 3 {−2 − (−5)}]

=1/2 [12 + 0 + 9]

= 21/2 sq. units

Again using formula to find area of triangle:

Area of △ACD = [−4 (−2 − 3) + 3 {3 − (−2)} + 2 {−2 − (-2)}]

= 1/2 [20 + 15 + 0]

= 35/2 sq. units

Area of ☐ABCD = Area of ΔABC + Area of ΔACD

                        = 21/2 + 35/2 = 28 sq. units

 

 

Let the vertices of the triangle be A (4, -6), B (3, -2), and C (5, 2).

Let D be the mid-point of side BC of ΔABC. Therefore, AD is the median in ΔABC.

Coordinates of point D = (3+5/2, -2+2/2) = (4,0)

Area of a triangle = 1/2 {x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2)}

Area of △ABD = 1/2[4 (−2 − 0) + 3 {0 − (−6)} + 4 {−6 − (−2)}]

=1/2(−8 + 18 −16)

=1/2 (−6) = −3 sq units

Area cannot be in negative.

Therefore, we just consider its numerical value.

Therefore, area of △ABD = 3 sq units

Again using formula to find area of triangle:

Area of △ABD = 1/2 [4 (0 − 2) + 4{2 − (−6)} + 5 {−6 −0 )}]

 = 1/2 (- 8 + 32 −30) = ½ (-6) = -3 sq units.

However, area cannot be negative. Therefore, area of ΔABD is 3 square units.

The area of both sides is same. Thus, median AD has divided ΔABC in two triangles of equal areas

Hence Proved.

 

P is the mid point of side AB

Therefore the coordinates of P are ((-1-1)/2,(-1+4)/2) = (-1, 3/2)

Similary the coordinates of Q , R and S are  (2,4),(5, 3/2), and (2, -1) respectilvely

Length of PQ =

Length of QR =

Length of RS =

Length of SP =

Length of PR == 6

Length of QS == 5

It can be observed that all sides of the given quadrilateral are of the same measure. However, the diagonals are of different lengths. Therefore, PQRS is a rhombus

 

Let the given line divide the line segment joining the points A(2, −2) and B(3, 7) in a ratio k : 1

Coordinates of the point of division =

This point also lies on 2x + y - 4 = 0

⇒

⇒

⇒  9k - 2 = 0

⇒  k = 2/9

Therefore, the ratio in which the line 2x + y - 4 = 0  divides the line segment joining the points A(2, −2) and B(3, 7) is 2:9.

 

If the given points are collinear, then the area of triangle formed by these points will be 0.

Area of triangle =

 Area =

0 = 1/2 [2x - y + 7y - 14]

0 =1/2 [2x + 6y - 14]

[2x + 6y - 14] = 0

x + 3y - 7 = 0

This is the required relation between x & y.

 

 Let O (x,y) be the centre of the circle. And let the points (6, −6), (3, −7), and (3, 3) be representing the points A, B, and C on the circumference of the circle.

However OA = OB (Radii of same circle)

⇒

=>x² + 36 - 12x + y² + 36 + 12y = x² + 9 - 6x + y² + 49 -14y

⇒ -6x + 2y + 14 = 0

⇒ 3x + y = 7 ....1

Similary OA = OC (Radii of same circle)

=>x² + 36 - 12x + y² + 36 + 12y = x² + 9 - 6x + y² + 9 - 6y

⇒ -6x + 18y + 54 = 0

⇒ -3x + 9y = -27  .....(2)

On adding equation (1) and (2), we obtain

10y = - 20

y = - 2

From equation (1), we obtain

3x − 2 = 7

3x = 9

x = 3

Therefore, the centre of the circle is (3, −2).

 

(i) Taking A as the origin, AD and AB as the coordinate axes. Clearly, the points P, Q and

R are (4, 6), (3, 2) and (6, 5) respectively.

(ii)Taking C as the origin, CB and CD as the coordinate axes. Clearly, the points P, Q and R are given by (12, 2), (13, 6) and (10, 3) respectively.

We know that the area of the triangle (POR) =

= 1/2 [4(2-5) + 3(5-6) + 6(6-2)]

= 1/2 [-12 -3 +24]

= 9/2 sq. units

(ii) Taking C as origin, CB as x- axis, and CD as y- axis, the coordinates of vertices P, Q, and R are (12, 2), (13, 6), and (10, 3) respectively.

area of the triangle (PQR) =

= 1/2[12(6-3) + 13(3-2) + 10(2-6)

= 1/2 [36+13-40]

= 9/2 sq. units

Hence, the areas are the same in both cases.

 

Let ABCD be a square having (−1, 2) and (3, 2) as vertices A and C respectively. Let (x,y), (x1,y1) be the coordinate of vertex B and D respectively.

We know that the sides of a square are equal to each other.

∴ AB = BC

=>x² + 2x + 1 + y²  -4y + 4 = x² + 9  -6x + y² + 4 - 4y

⇒ 8x = 8

⇒ x = 1

We know that in a square, all interior angles are of 90°.

In ΔABC,

AB² + BC² = AC²

⇒4 + y² + 4 − 4y + 4 + y² + 4 − 4y = 16

⇒2y² + 16 − 8 = 16

⇒2y² - 8 = 0

⇒y(y - 4) = 0

⇒y = 0 or 4

We know that in a square, the diagonals are of equal length and bisect each other at 90°. Let O be the mid-point of AC. Therefore, it will also be the mid-point of BD

Coordinate of point O = ((-1+3)/2, (2+2)/2)

⇒1 + x1/2 = 1

⇒1 + x1 = 2

⇒x1 = 1

and y + y1 /2 = 2

⇒ y + y1= 4

⇒If y = 0

⇒y1= 4

⇒If y = 4

⇒y1= 0

Therefore, the required coordinates are (1, 0) and (1, 4).

 

Given that (AD)/(AB) = (AE)/(AC) = 1/4

(AD)/(AD+DB) = (AE)/(AE+EC) = 1/4

(AD)/(DB)=(AE)/(EC) = 1/3

Therefore, D and E are two points on side AB and AC respectively such that they divide side AB and AC in a ratio of 1:3

Coordinates of Point D == (13/4, 23/4)

Coordinates of Point E = = (19/4, 20/4)

Area of triangle =

Area of ΔADE =

 =

Area of ΔABC = 1/2[4(5-2) + 1(2-6) + 7(6-5)]

= 1/2[12 - 4 + 7]

= 15/2

Clearly, the ratio between the areas of ΔADE and ΔABC is 1:16.

 

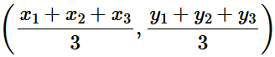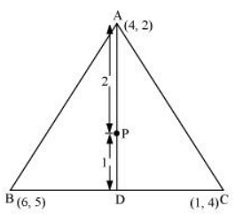
(i) Median AD of the triangle will divide the side BC in two equal parts.

Therefore, D is the mid-point of side BC

Coordinate of D = (6 +1/2, 5 + 4/2) =(7/2,9/2)

(ii) Point P divides the side AD in a ratio 2:1.

Coordinate of P = 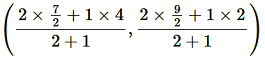= (11/3 , 11/3)

(iii) Median BE of the triangle will divide the side AC in two equal parts.

Therefore, E is the mid-point of side AC.

Coordinate of E = (4+1/2, 2+4/2) = (5/2,3)

Point Q divides the side BE in a ratio 2:1.

Coordinate of Q =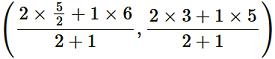= (11/3 , 11/3)

Median CF of the triangle will divide the side AB in two equal parts. Therefore, F is the mid-point of side AB

Coordinate of F = (4+6/2, 2+5/2) = (5,7/2)

Point R divides the side CF in a ratio 2:1.

Coordinate of R =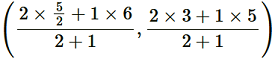= (11/3 , 11/3)

(iv) It can be observed that the coordinates of point P, Q, R are the same.

Therefore, all these are representing the same point on the plane i.e., the centroid of the triangle.

(v) Consider a triangle, ΔABC, having its vertices as A(x1,y1), B(x2,y2) and C(x3,y3)

Median AD of the triangle will divide the side BC in two equal parts. Therefore, D is the mid-point of side BC.

Coordinate of D =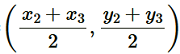

Let the centroid of this triangle be O.

Point O divides the side AD in a ratio 2:1.

Coordinate of O =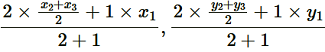

=