NCERT Solutions for Class 10 Maths Chapter 5: Arithmetic Progressions

(i) It can be observed that
Taxi fare for 1st km = 15
Taxi fare for first 2 km = 15 + 8 = 23
Taxi fare for first 3 km = 23 + 8 = 31
Taxi fare for first 4 km = 31 + 8 = 39
Clearly 15, 23, 31, 39 … forms an A.P. because every term is 8 more than the preceding term.

(ii) Let the initial volume of air in a cylinder be V litres. In each stroke, the vacuum pump removes 1/4 of air remaining in the cylinder at a time. In other words, after every stroke, only 1 - 1/4 = 3/4th part of air will remain.
Therefore, volumes will be V, 3V/4 , (3V/4)2 , (3V/4)3...
Clearly, it can be observed that the adjacent terms of this series do not have the same difference between them. Therefore, this is not an A.P.

 

(iii)   Cost of digging for first metre = 150
Cost of digging for first 2 metres = 150 + 50 = 200
Cost of digging for first 3 metres = 200 + 50 = 250
Cost of digging for first 4 metres = 250 + 50 = 300
Clearly, 150, 200, 250, 300 … forms an A.P. because every term is 50 more than the preceding term.

 

(iv) We know that if Rs P is deposited at r% compound interest per annum for n years, our money will be

Therefore, after every year, our money will be

 

It is not an arithmetic progression because (2) − (1) ≠ (3) − (2)

(Difference between consecutive terms is not equal)

Therefore, it is not an Arithmetic Progression.

 

 

(i) a = 10, d = 10
Let the series be a1, a2, a3, a4, a5 …
a1 = a = 10
a2 = a1 + d = 10 + 10 = 20
a3 = a2 + d = 20 + 10 = 30
a4 = a3 + d = 30 + 10 = 40
a5 = a4 + d = 40 + 10 = 50
Therefore, the series will be 10, 20, 30, 40, 50 …
First four terms of this A.P. will be 10, 20, 30, and 40.

(ii) a = - 2, d = 0
Let the series be a1, a2, a3, a4 …
a1 = a = -2
a2 = a1 + d = - 2 + 0 = - 2
a3 = a2 + d = - 2 + 0 = - 2
a4 = a3 + d = - 2 + 0 = - 2
Therefore, the series will be - 2, - 2, - 2, - 2 …
First four terms of this A.P. will be - 2, - 2, - 2 and - 2.

(iii) a = 4, d = - 3
Let the series be a1, a2, a3, a4 …
a1 = a = 4
a2 = a1 + d = 4 - 3 = 1
a3 = a2 + d = 1 - 3 = - 2
a4 = a3 + d = - 2 - 3 = - 5
Therefore, the series will be 4, 1, - 2 - 5 …
First four terms of this A.P. will be 4, 1, - 2 and - 5.

(iv) a = - 1, d = 1/2
Let the series be a1, a2, a3, a4 …a1 = a = -1
a2 = a1 + d = -1 + 1/2 = -1/2
a3 = a2 + d = -1/2 + 1/2 = 0
a4 = a3 + d = 0 + 1/2 = 1/2
Clearly, the series will be-1, -1/2, 0, 1/2
First four terms of this A.P. will be -1, -1/2, 0 and 1/2.

(v) a = - 1.25, d = - 0.25
Let the series be a1, a2, a3, a4 …
a1 = a = - 1.25
a2 = a1 + d = - 1.25 - 0.25 = - 1.50
a3 = a2 + d = - 1.50 - 0.25 = - 1.75
a4 = a3 + d = - 1.75 - 0.25 = - 2.00
Clearly, the series will be 1.25, - 1.50, - 1.75, - 2.00 ……..
First four terms of this A.P. will be - 1.25, - 1.50, - 1.75 and - 2.00.

 

 

(i) 3, 1, - 1, - 3 …
Here, first term, a = 3
Common difference, d = Second term - First term
= 1 - 3 = - 2

(ii) - 5, - 1, 3, 7 …
Here, first term, a = - 5
Common difference, d = Second term - First term
= ( - 1) - ( - 5) = - 1 + 5 = 4
(iii) 1/3, 5/3, 9/3, 13/3 ....
Here, first term, a = 1/3
Common difference, d = Second term - First term
= 5/3 - 1/3 = 4/3

(iv) 0.6, 1.7, 2.8, 3.9 …
Here, first term, a = 0.6
Common difference, d = Second term - First term
= 1.7 - 0.6
= 1.1

(i) 2, 4, 8, 16 …
Here,
a2 - a1 = 4 - 2 = 2
a3 - a2 = 8 - 4 = 4
a4 - a3 = 16 - 8 = 8
⇒ an+1 - an is not the same every time.
Therefore, the given numbers are forming an A.P.

(ii) 2, 5/2, 3, 7/2 ....
Here,
a2 - a1 = 5/2 - 2 = 1/2
a3 - a2 = 3 - 5/2 = 1/2
a4 - a3 = 7/2 - 3 = 1/2
⇒ an+1 - an is same every time.
Therefore, d = 1/2 and the given numbers are in A.P.
Three more terms are
a5 = 7/2 + 1/2 = 4
a6 = 4 + 1/2 = 9/2
a7 = 9/2 + 1/2 = 5

(iii) -1.2, - 3.2, -5.2, -7.2 …
Here,
a2 - a1 = ( -3.2) - ( -1.2) = -2
a3 - a2 = ( -5.2) - ( -3.2) = -2
a4 - a3 = ( -7.2) - ( -5.2) = -2
⇒ an+1 - an is same every time.
Therefore, d = -2 and the given numbers are in A.P.
Three more terms are
a5 = - 7.2 - 2 = - 9.2
a6 = - 9.2 - 2 = - 11.2
a7 = - 11.2 - 2 = - 13.2

(iv) -10, - 6, - 2, 2 …
Here,
a2 - a1 = (-6) - (-10) = 4
a3 - a2 = (-2) - (-6) = 4
a4 - a3 = (2) - (-2) = 4
⇒ an+1 - an is same every time.
Therefore, d = 4 and the given numbers are in A.P.
Three more terms are
a5 = 2 + 4 = 6
a6 = 6 + 4 = 10
a7 = 10 + 4 = 14

(v) 3, 3 + √2, 3 + 2√2, 3 + 3√2
Here,
a2 - a1 = 3 + √2 - 3 = √2
a3 - a2 = (3 + 2√2) - (3 + √2) = √2
a4 - a3 = (3 + 3√2) - (3 + 2√2) = √2
⇒ an+1 - an is same every time.
Therefore, d = √2 and the given numbers are in A.P.
Three more terms are
a5 = (3 + √2) + √2 = 3 + 4√2
a6 = (3 + 4√2) + √2 = 3 + 5√2
a7 = (3 + 5√2) + √2 = 3 + 6√2

(vi) 0.2, 0.22, 0.222, 0.2222 ….
Here,
a2 - a1 = 0.22 - 0.2 = 0.02
a3 - a2 = 0.222 - 0.22 = 0.002
a4 - a3 = 0.2222 - 0.222 = 0.0002
⇒ an+1 - an is not the same every time.
Therefore, the given numbers are forming an A.P.

(vii) 0, -4, -8, -12 …
Here,
a2 - a1 = (-4) - 0 = -4
a3 - a2 = (-8) - (-4) = -4
a4 - a3 = (-12) - (-8) = -4
⇒ an+1 - an is same every time.
Therefore, d = -4 and the given numbers are in A.P.
Three more terms are
a5 = -12 - 4 = -16
a6 = -16 - 4 = -20
a7 = -20 - 4 = -24

(viii) -1/2, -1/2, -1/2, -1/2 ....
Here,
a2 - a1 = (-1/2) - (-1/2) = 0
a3 - a2 = (-1/2) - (-1/2) = 0
a4 - a3 = (-1/2) - (-1/2) = 0
⇒ an+1 - an is same every time.
Therefore, d = 0 and the given numbers are in A.P.
Three more terms are
a5 = (-1/2) - 0 = -1/2
a6 = (-1/2) - 0 = -1/2
a7 = (-1/2) - 0 = -1/2

(ix) 1, 3, 9, 27 …
Here,
a2 - a1 = 3 - 1 = 2
a3 - a2 = 9 - 3 = 6
a4 - a3 = 27 - 9 = 18
⇒ an+1 - an is not the same every time.
Therefore, the given numbers are forming an A.P.

(x) a, 2a, 3a, 4a …
Here,
a2 - a1 = 2a - a = a
a3 - a2 = 3a - 2a = a
a4 - a3 = 4a - 3a = a
⇒ an+1 - an is same every time.
Therefore, d = a and the given numbers are in A.P.
Three more terms are
a5 = 4a + a = 5a
a6 = 5a + a = 6a
a7 = 6a + a = 7a

(xi) a, a2, a3, a4 …
Here,
a2 - a1 = a2 - a = (a - 1)
a3 - a2 = a3 - a2 = a2 (a - 1)
a4 - a3 = a4 - a3 = a3(a - 1)
⇒ an+1 - an is not the same every time.
Therefore, the given numbers are forming an A.P.

(xii) √2, √8, √18, √32 ...
Here,
a2 - a1 = √8 - √2  = 2√2 - √2 = √2
a3 - a2 = √18 - √8 = 3√2 - 2√2 = √2
a4 - a3 = 4√2 - 3√2 = √2
⇒ an+1 - an is same every time.
Therefore, d = √2 and the given numbers are in A.P.
Three more terms are
a5 = √32  + √2 = 4√2 + √2 = 5√2 = √50
a6 = 5√2 +√2 = 6√2 = √72
a7 = 6√2 + √2 = 7√2 = √98

(xiii) √3, √6, √9, √12 ...
Here,
a2 - a1 = √6 - √3 = √3 × 2 -√3 = √3(√2 - 1)
a3 - a2 = √9 - √6 = 3 - √6 = √3(√3 - √2)
a4 - a3 = √12 - √9 = 2√3 - √3 × 3 = √3(2 - √3)
⇒ an+1 - an is not the same every time.
Therefore, the given numbers are forming an A.P.

(xiv) 12, 32, 52, 72 …
Or, 1, 9, 25, 49 …..
Here,
a2 − a1 = 9 − 1 = 8
a3 − a2 = 25 − 9 = 16
a4 − a3 = 49 − 25 = 24
⇒ an+1 - an is not the same every time.
Therefore, the given numbers are forming an A.P.

(xv) 12, 52, 72, 73 …
Or 1, 25, 49, 73 …
Here,
a2 − a1 = 25 − 1 = 24
a3 − a2 = 49 − 25 = 24
a4 − a3 = 73 − 49 = 24
i.e., ak+1 − ak is same every time.
⇒ an+1 - an is same every time.
Therefore, d = 24 and the given numbers are in A.P.
Three more terms are
a5 = 73+ 24 = 97
a6 = 97 + 24 = 121
a7 = 121 + 24 = 145

(i) 140 = 2 x 2 x 5 x 7 = 22 x 5 x 7

(ii) 156 = 2 x 2 x 3 x 13 = 22 x 3 x 13

(iii) 3825 = 3 x 3 x 5 x 17 = 32 x 52 x x 17

(iv) 5005 = 5 x 7 x 11 x 13

(v) 7429 = 17 x 19 x 23 

 

HCF (306, 657) = 9

We know that, LCM × HCF = Product of two numbers

L.C.M x  H.C.F = first Number x Second Number

L.C.M x 9 = 306 x 657

LCM = 22338

 

TO CHECK: Whether 62can end with the digit 0 for any natural number n.

We know that

62 = (2 × 3)n

62 = (2)n ×(3)n

Therefore, prime factorization of 6ndoes not contain 5 and 2 as a factor together.

Hence 6n can never end with the digit 0 for any natural number n

 

So, the given expression has 6 and 13 as its factors. Therefore, we can conclude that it is a composite number.

Similarly,

7 x 6 x 5 x 4 x 3 x 2 x 1 + 5

= 5 x (7 x 6 x 4 x 3 x 2 x 1 + 1) [taking 5 out- common]

= 5 x (1008 + 1)

= 5 x 1009

Since, 1009 is a prime number the given expression has 5 and 1009 as its factors other than 1 and the number itself.

Hence, it is also a composite number.

 

(i) 26 and 91

a = 26, b = 91

∴ H.C.F = 13

L.C.M = 2 × 7 × 13

= 14 × 13 = 182

∴ H.C.F × L.C.M = a × b

13 × 182 = 26 × 96

2366 = 2366

(ii) 510 and 92

a = 510, b = 92

(iii) 336 and 54

a = 336, b = 54Read more on Sarthaks.com - https://www.sarthaks.com/661852/find-the-lcm-and-the-following-pairs-integers-and-verify-that-lcm-hcf-product-the-two-numbers

336= 2 x 2 x 2 x 2 x 3 x 7 = 24 x 3 x 7

54 = 2 x 3 x 3 x 3 = 2 x 33

HCF = 2 x 3 = 6

LCM = 24 x 33 x 7= 3024

Product of two numbers 336 and 54 = 336 x 54= 18144

3024 x 6= 18144

Hence, product of two numbers = 18144

 

(i) 12, 15 and 21

12 = 2 × 2 × 3 = 22× 3

15 = 3 × 5

and 21 = 3 × 7

For HCF, we find minimum power of prime factor

H.C.F. = (3)1= 3

For LCM, taking maximum power of prime factors

L.C.M. = 22 × 3 × 5 × 7 = 4 × 3 × 5 × 7 = 420

So,H.C.F. = (3)1= 3

and L.C.M. =  420

(ii) 17, 23 and 29

17 = 1 × 17

23 = 1 x 23

29 = 1 x 29

For HCF, common factor is 1

HCF = 1

For LCM taking maximum power of prime factor.

L.C.M. = 1 × 17 × 23 × 29 = 11339

So H.C.F. = 1

L.C.M. = 11339

(iii) 8, 9 and 25

8 = 2 × 2 × 2 × 1 = 23× 1

9 = 3 × 3 = 32

and 25 = 5 × 5 = 52

For HCF common factor is 1

H.C.F. = 1

For LCM, taking maximum power of prime factors

L.C.M. = 23× 32 × 52

= 8 × 9 × 25 = 1800

So H.C.F. = 1

L.C.M. = 1800

 

 

It can be observed that Ravi takes less time than Sonia for completing 1 round of the circular path. As they are going in the same direction, they will meet again at the same time when Ravi will have completed 1 round of that circular path with respect to Sonia. And the total time taken for completing this 1 round of circular path will be the LCM of time taken by Sonia and Ravi for completing 1 round of circular path respectively i.e., LCM of 18 minutes and 12 minutes.

LCM of 12 and 18= 2 x 2 x 3 x 3 = 36

Therefore, Ravi and Sonia will meet together at the starting point after 36 minutes.

 

It is given that the sum of n terms of an AP is equal to

It means

So here, we can find the first term by substituting n = 1 ,

=4-1=3

Similarly, the sum of first two terms can be given by,

= 8 - 4

= 4

Now, as we know,

 

So,

 

 = 4 - 3

= 1

Now, using the same method we have to find the third, tenth and nth term of A.P.

So, for the third term,

 

=

= (12 - 9) - (8 - 4)

= 3 - 4

= - 1

Also, for the tenth term,

=

= (40 - 100) - (36 - 81)

= - 60 + 45

= 15

So, for the nth term,

=

=

=

= 5 - 2n

Therefore,=

 

The distance of potatoes are as follows :

5, 8, 11, 14, .....

It can be observed that these distances are in A.P.

  a = 5

 d =  8 - 5 = 3

From the formula, we get

=

= 5 [10 + 9 x 3]

= 5 (10 + 27)

= 5 x 37

= 185

 As every time she has to run back to the bucket, therefore, the total distance that the competitor has to run will be two times of it.

Therefore, the total distance that the competitor will run = 2 x 185 = 370m.

 

(i) 2, 7, 12… to 10 terms

Here First term = a = 2, Common difference = d = 7 – 2 = 5 and n = 10

Applying formula,to find sum of n terms of AP,

(ii) –37, –33, –29… to 12 terms

Here First term = a = –37, Common difference = d = –33 – (–37) = 4

And n = 12

Applying formula,to find sum of n terms of AP,

(iii) 0.6, 1.7, 2.8… to 100 terms

Here First term = a = 0.6, Common difference = d = 1.7 – 0.6 = 1.1

And n = 100

Applying formula,to find sum of n terms of AP,

(iv) to 11 terms

Here First tern =a = 1/15Common difference =

Applying formula,to find sum of n terms of AP,

 

 

(i)

Here First term = a = 7, Common difference = d =

And Last term = l = 84

We do not know how many terms are there in the given AP.

So, we need to find n first.

Using formula , to find nth term of arithmetic progression,

[7 + (n − 1) (3.5)] = 84

⇒ 7 + (3.5) n − 3.5 = 84

⇒ 3.5n = 84 + 3.5 – 7

⇒ 3.5n = 80.5

⇒ n = 23

Therefore, there are 23 terms in the given AP.

It means n = 23.

Applying formula, to find sum of n terms of AP,

(ii) 34 + 32 + 30 + … + 10

Here First term = a = 34, Common difference = d = 32 – 34 = –2

And Last term = l = 10

We do not know how many terms are there in the given AP.

So, we need to find n first.

Using formula , to find nth term of arithmetic progression,

[34 + (n − 1) (−2)] = 10

⇒ 34 – 2n + 2 = 10

⇒ −2n = −26⇒ n = 13

Therefore, there are 13 terms in the given AP.

It means n = 13.

Applying formula, to find sum of n terms of AP,

(iii) −5 + (−8) + (−11) + … + (−230)

Here First term = a = –5, Common difference = d = –8 – (–5) = –8 + 5 = –3

And Last term = l = −230

We do not know how many terms are there in the given AP.

So, we need to find n first.

Using formula , to find nth term of arithmetic progression,

[−5 + (n − 1) (−3)] = −230

⇒ −5 − 3n + 3 = −230

⇒ −3n = −228 ⇒ n = 76

Therefore, there are 76 terms in the given AP.

It means n = 76.

Applying formula, to find sum of n terms of AP,

 

 

i) Given a =( 5, d = 3, an = 50,find n and Sn.

Using formula an = a + (n-1)d, to find nth term of arithmetic progression,

⇒ 50 = 5 + (n − 1) (3)

⇒ 50 = 5 + 3n − 3

⇒ 48 = 3n⇒ n = 16

Applying formula,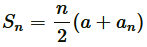to find sum of n terms of AP,

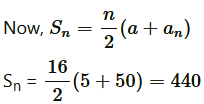
Therefore, n = 16 and Sn  = 440

(ii) Given a = 7, a13 = 35, find d and S13..

Using formula an = a + (n-1)d, to find nth term of arithmetic progression,

an = a + (n-1)d

a13= 7 + (13 − 1) (d)

⇒ 35 = 7 + 12d

⇒ 28 = 12d⇒ d = 28/12 = 7/3

Applying formula,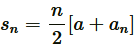to find sum of n terms of AP,

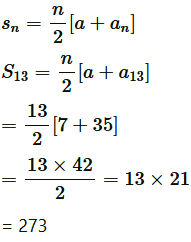
Therefore, d = 7/3 and S13 = 273

(iii) Given a12 = 37, d = 3, find a and S12..

Using formula an = a + (n-1)d, to find nth term of arithmetic progression,

an = a + (n-1)d

a12 = a + (12 − 1) 3

⇒ 37 = a + 33 ⇒ a = 4

Applying formula,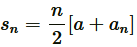to find sum of n terms of AP,

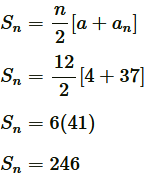
Therefore, a = 4 and S12 = 246

(iv) Given a3 = 15, S10 = 125, find d and a10..

Using formula an = a + (n-1)d, to find nth term of arithmetic progression,

an = a + (n-1)d

a3 = a + (3 − 1) (d)

⇒ 15 = a + 2d

⇒ a = 15 − 2d… (1)

Applying formula,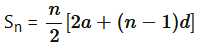to find sum of n terms of AP,

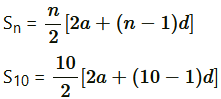
⇒ 125 = 5 (2a + 9d) = 10a + 45d

Putting (1) in the above equation,

125 = 5 [2 (15 − 2d) + 9d] = 5 (30 − 4d + 9d)

⇒ 125 = 150 + 25d

⇒ 125 – 150 = 25d

⇒ −25 = 25d⇒ d = −1

Using formula an = a + (n-1)d, to find nth term of arithmetic progression,

an = a + (n-1)d

a10= a + (10 − 1) d

Putting value of d and equation (1) in the above equation,

a10= 15 − 2d + 9d = 15 + 7d

= 15 + 7 (−1) = 15 – 7 = 8

Therefore, d = −1 and a10= 8

(v) Given d = 5,S9 = 75, find a and a9..

Applying formula,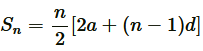to find sum of n terms of AP,

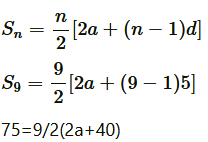
⇒ 150 = 18a + 360

⇒ −210 = 18a

⇒ a =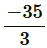

Using formula an = a + (n-1)d, to find nth term of arithmetic progression,

a9 = 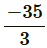+ (9 − 1) (5)

a9 =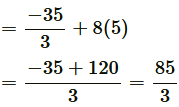

Therefore, a = 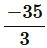and a9 =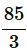

(vi) Given a = 2, d = 8, Sn = 90, find n and an.

Applying formula,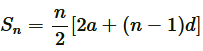to find sum of n terms of AP,

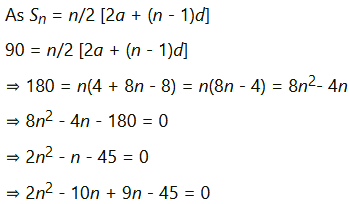
⇒ 2n (n − 5) + 9 (n − 5) = 0

⇒ (n − 5) (2n + 9) = 0

⇒ n = 5,−9/2

We discard the negative value of n because here n cannot be in negative or fraction.

The value of n must be a positive integer.

Therefore, n = 5

Using formula an = a + (n-1)d ,to find nth term of arithmetic progression,

a5 = 2 + (5 − 1) (8) = 2 + 32 = 34

Therefore, n = 5 and a5 = 34

(vii) Given a = 8, an = 62, Sn = 210, find n and d.

Using formula an = a + (n-1)d, to find nth term of arithmetic progression,

62 = 8 + (n − 1) (d) = 8 + nd – d

⇒ 62 = 8 + nd − d

⇒ nd – d = 54

⇒ nd = 54 + d… (1)

Applying formula,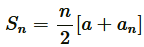to find sum of n terms of AP,

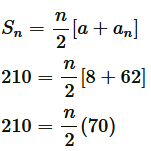
⇒ n = 6

Putting value of n in equation (1),

6d = 54 + d ⇒ d =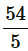

Therefore, n = 6 and d =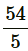

(viii) Given Given an = 4, d = 2, Sn = − 14, find n and a

Using formula an = a + (n-1)d , to find nth term of arithmetic progression,

4 = a + (n − 1) (2) = a + 2n − 2

⇒ 4 = a + 2n – 2

⇒ 6 = a + 2n

⇒ a = 6 − 2n… (1)

Applying formula,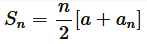to find sum of n terms of AP,

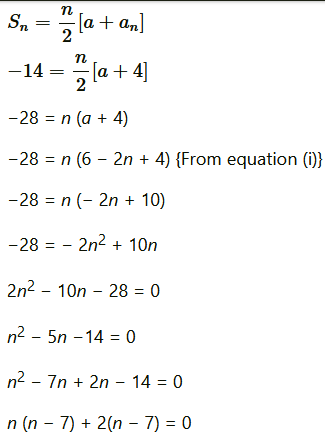
⇒ (n + 2) (n − 7) = 0

⇒ n = −2, 7

Here, we cannot have a negative value of n.

Therefore, we discard the negative value of n which means n = 7.

Putting value of n in equation (1), we get

a = 6 − 2n = 6 – 2 (7) = 6 – 14 = −8

Therefore, n = 7 and a = −8

(ix)Given a = 3, n = 8, S = 192, find d.

Using formula, an = a + (n-1)d to find sum of n terms of AP, we get

192 = 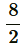[6 + (8 − 1) d] = 4 (6 + 7d)

⇒ 192 = 24 + 28d

⇒ 168 = 28d ⇒ d = 6

(x) Given l = 28, S = 144, and there are total of 9 terms. Find a.

Applying formula, 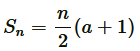, to find sum of n terms, we get

144 = 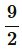[a + 28]

⇒ 288 = 9 [a + 28]

⇒ 32 = a + 28⇒ a = 4

First term = a = 9, Common difference = d = 17 – 9 = 8, Sn = 636

Applying formula,to find sum of n terms of AP, we get

636 =[18 + (n − 1) (8)]

⇒ 1272 = n (18 + 8n − 8)

⇒

We discard the negative value of n here because n cannot be in negative, n can only be a positive integer.

Therefore, n = 12

Therefore, 12 terms of the given sequence make the sum equal to 636.

First term = a = 5, Last term = l = 45,

Applying formula, to find sum of n terms of AP, we get

⇒ n = 16

Applying formula,to find sum of n terms of AP and putting value of n, we get

We get,

45 = 5 + (16 - 1)d

45 = 5 + (15)d

45 - 5 = 15d

 

 

First term = a = 17, Last term = l = 350 and Common difference = d = 9

Using formula , to find nth term of arithmetic progression, we get

350 = 17 + (n − 1) (9)

⇒ 350 = 17 + 9n − 9

⇒ 342 = 9n ⇒ n = 38

Applying formula,to find sum of n terms of AP and putting value of n, we get

 =19 (34 + 333) = 6973

Therefore, there are 38 terms and their sum is equal to 6973.

It is given that 22nd term is equal to 149

Using formula an = a + (n-1)d, to find nth term of arithmetic progression, we get

an = a + (n-1)d

149 = a + (22 − 1) (7)

⇒ 149 = a + 147⇒ a = 2

Applying formula,to find sum of n terms of AP and putting value of a, we get

= 11 (4 + 147)

⇒ 11(151)= 1661

Therefore, the sum of the first 22 terms of AP is equal to 1661.

It is given that second and third term of AP are 14 and 18 respectively.

Using formula an = a + (n-1)d, to find nth term of arithmetic progression, we get

14 = a + (2 − 1) d

⇒ 14 = a + d … (1)

And, 18 = a + (3 − 1) d

⇒ 18 = a + 2d … (2)

These are equations consisting of two variables.

Using equation (1), we get, a = 14 − d

Putting value of a in equation (2), we get

18 = 14 – d + 2d

⇒ d = 4

Therefore, common difference d = 4

Putting value of d in equation (1), we get

18 = a + 2 (4)

⇒ a = 10

Applying formula,to find sum of n terms of AP, we get

Therefore, sum of first 51 terms of an AP is equal to 5610.

It is given that sum of first 7 terms of an AP is equal to 49 and sum of first 17 terms is equal to 289.

Applying formula,to find sum of n terms of AP, we get

⇒ 98 = 7 (2a + 6d)

⇒ 7 = a + 3d ⇒ a = 7 − 3d … (1)

And, s17= 289

⇒ 578 = 17 (2a + 16d)

⇒ 34 = 2a + 16d

⇒ 17 = a + 8d

Putting equation (1) in the above equation, we get

17 = 7 − 3d + 8d

⇒ 10 = 5d ⇒ d = 2

Putting value of d in equation (1), we get

a = 7 − 3d = 7 – 3 (2) = 7 – 6 = 1

Again applying formula,to find sum of n terms of AP, we get

 

 

(i)

is the same every time. Therefore, this is an AP with a common difference as 4 and first term as 7.

Therefore, sum of first 15 terms of AP is equal to 525.

(ii)

is the same every time. Therefore, this is an AP with a common difference as -5 and first term as 4.

 

Therefore, sum of the first 15 terms of AP is equal to –465.

 

The first positive integers that are divisible by 6 are 6, 12, 18, 24 … 40 terms.

Therefore, we want to find sum of 40 terms of sequence of the form:

6, 12, 18, 24 … 40 terms

Here, first term = a = 6 and Common difference = d = 12 – 6 = 6, n = 40

Applying formula, to find sum of n terms of AP, we get

a = 6

d = 6

S40 = ?

=

= 20 [12 + (39) (6 )]

= 20 (12 + 234)

= 20 x 246

= 4920

 

The first 15 multiples of 8 are 8,16, 24, 32 … 15 times

First term = a = 8 and Common difference = d = 16 – 8 = 8, n = 15

Applying formula, to find sum of n terms of AP, we get

I  = a + (n-1) d

  = 8 + (15 - 1) 8

 = 120

Required Sum =

 =

Hence, the required sum is 960.

 

 

The odd numbers between 0 and 50 are 1, 3, 5, 7 … 49

It is an arithmetic progression because the difference between consecutive terms is constant.

First term = a = 1, Common difference = 3 – 1 = 2, Last term = l = 49

We do not know how many odd numbers are present between 0 and 50.

Therefore, we need to find n first.

Using formula an = a + (n − 1) d, to find nth term of arithmetic progression, we get

49 = 1 + (n − 1) 2

⇒ 49 = 1 + 2n − 2

⇒ 50 = 2n ⇒ n = 25

Applying formula, to find sum of n terms of AP, we get

=

=

= 625

Penalty for first day = Rs 200, Penalty for second day = Rs 250

Penalty for third day = Rs 300

It is given that the penalty for each succeeding day is Rs 50 more than the preceding day.

It makes it an arithmetic progression because the difference between consecutive terms is constant.

We want to know how much money the contractor has to pay as penalty, if he has delayed the work by 30 days.

So, we have an AP of the form 200, 250, 300, 350 … 30 terms

First term = a = 200, Common difference = d = 50, n = 30

Applying formula, to find sum of n terms of AP, we get

⇒

⇒ 15 (400 + 1450)

 = 15 x 1850

 = 27750

Therefore, the penalty for 30 days is Rs. 27750.

It is given that the sum of seven cash prizes is equal to Rs 700.

And, each prize is R.s 20 less than its preceding term.

Let value of first prize = Rs. a

Let value of second prize =Rs (a − 20)

Let value of third prize = Rs (a − 40)

So, we have sequence of the form:

a, a − 20, a − 40, a – 60 …

It is an arithmetic progression because the difference between consecutive terms is constant.

First term = a, Common difference = d = (a – 20) – a = –20

n = 7 (Because there are total of seven prizes)

Applying formula, to find sum of n terms of AP, we get

=

⇒

=

= 700 = 7 (a - 60)

On further specification, we get

 ⇒ 700/7 = a - 60

⇒ 100 + 60 = a

⇒  a = 160

Therefore, value of first prize = Rs 160

Value of second prize = 160 – 20 = Rs 140

Value of third prize = 140 – 20 = Rs 120

Value of fourth prize = 120 – 20 = Rs 100

Value of fifth prize = 100 – 20 = Rs 80

Value of sixth prize = 80 – 20 = Rs 60

Value of seventh prize = 60 – 20 = Rs 40

 

There are three sections of each class and it is given that the number of trees planted by any class is equal to class number.

The number of trees planted by class I = number of sections

The number of trees planted by class II = number of sections

The number of trees planted by class III = number of sections

Therefore, we have sequence of the form 3, 6, 9 … 12 terms

To find the total number of trees planted by all the students, we need to find the sum of the sequence 3, 6, 9, 12 … 12 terms.

First term = a = 3, Common difference = d= 6 – 3 = 3 and n = 12

Applying formula, to find sum of n terms of AP , we get

=

= 6 (2+11)

= 6 x 13

= 78

Therefore, number of trees planted by 1 section of classes = 78

number of trees planted by 3 section of classes = 3 x 78 = 234

Therefore, 234 trees will be planted by the students.

 

 

Length of Semi-perimeter of circle = πr

Length of semi-circle of radii 0.5 cm = π(0.5) cm = π/2

Length of semi-circle of radii 1.0 cm = π(1.0) cm

Length of semi-circle of radii 1.5 cm = π(1.5) cm = 3π/2

Therefore, we have sequence of the form:

π(0.5), π(1.0), π(1.5) … 13 terms {There are a total of thirteen semi–circles}.

To find total length of the spiral, we need to find sum of the sequence π(0.5), π(1.0), π(1.5) … 13 terms

First term = a = 0.5, Common difference = 1.0 – 0.5 = 0.5 and n = 13

Applying formula, to find sum of n terms of AP, we get

=

=

= (13/2) (7π)

= (91π / 2)

= ((91 x 22) / 2) x (7)

= (13 x 11)

= 143

Therefore, the lenght of such a spiral of 13 consecutive semi - circles will be 143 cm.

 

The number of logs in the bottom row = 20

The number of logs in the next row = 19

The number of logs in the next to next row = 18

Therefore, we have a sequence of the form 20, 19, 18 …

First term = a = 20, Common difference = d = 19 – 20 = - 1

We need to find how many rows make a total of 200 logs.

Applying formula, to find sum of n terms of AP, we get

=

⇒ 400 = n (40 – n + 1)

⇒ 400 = n (41 - n)

⇒ 400 = 41n - n²

⇒ n² - 41n + 400 = 0

⇒ n² - 16n -25n + 400 = 0

⇒ n (n - 16) - 25 (n - 16) = 0

⇒ (n - 16) (n - 25) = 0

Either (n - 16) = 0 or n - 25 = 0

⇒ n = 16 or n = 25

⇒ an  = a + (n - 1)d

⇒ a16 = 20 + (16 - 1) (- 1)

⇒ a16 = 20 - 15

⇒ a16 = 5

Similarly,

⇒ a25 = 20 + (25 - 1) (- 1)

⇒ a25 = 20 - 24

 = - 4

Clearly, the number of logs in the 16th row is 5. However, the number of logs in 25th row is negative, which is not possible.

Therefore,  200 logs can be placed in 16 rows and the number of logs in the 16th row is 5.

 

Given: 121, 117, 113, …….

Here, a = 121 and d = 117-121 = - 4

Let the nth term of the given A.P. be the first negative term. Then, an  < 0.

⇒ 121+ (n - 1) x (- 4) < 0                                [  an = a + (n - 1) d]

⇒ 125 - 4n < 0

⇒ - 4n < -125

⇒

Therefore, n = 32

Hence, the first negative term is the 32nd term.

We know that,

⇒ an = a + (n - 1) d

⇒ a3 = a + (3 - 1) d

⇒ a3 = a + 2d

Similarly,   a7 = a + 6d

Given,      a3 + a7 = 6

⇒ (a + 2d) + (a + 6d) = 6

⇒ 2a + 8d = 6

⇒ a + 4d = 3

⇒ a = 3 - 4d  (i)

Also, it is given that, (a3) x (a7) = 8

⇒ (a + 2d)  x (a + 6d) = 8

From Equation (i),

⇒  (3 - 4d + 2d ) x (3 - 4d + 6d) = 8

⇒  (3 - 2d) x (3 + 2d) = 8

⇒   9 - 4d² = 8

⇒   4d² = 9 - 8 = 1

⇒ d² = 1/4

⇒ d = ± 1/2

⇒ d = 1/2 or 1/2

From equation (i)

(When d = 1/2)

⇒ a = 3 - 4d

⇒ a = 3 - 4(1/2)

⇒ 3 - 2 = 1

(When d is - 1/2)

⇒ a = 3 - 4(-1/2)

⇒ a = 3 + 2 = 5

(When a is 1 & d is 1/2)

 

⇒   8 = [2 + 15/2]

⇒  4 (19) = 76

(When a is 5 & d is  - 1/2)

⇒ 8 [10 + (15(-1/2))]

⇒ 8 (5/2)

⇒ 20

 

 

It is given that the rungs are 25 cm apart and the top and bottom rungs are 2 1/2 m apart.

Therefore,Now, as the lengths of the rungs decrease uniformly, they will be in an A.P.

The length of the wood required for the rungs equals the sum of all the terms of this A.P.

First term, a = 45

Last term, l = 25

n = 11

⇒ Sn = n/2(a+1)

Therefore,S10 = 11/2(45+25) = 11/2 + 70 = 385cm.

Therefore, the length of the wood required for the rungs is 385 cm.

Let there be a value of x  such that the sum of the numbers of the houses preceding the houses numbered x is equal to the sum of the numbers of the houses following it.

That is , 1 + 2 + 3..... + (x + 1) = (x + 1) + (x + 2).........  + 49

Therefore, 1 + 2 + 3..... + (x + 1) = [1 + 2 + ..... + x + (x + 1)...... + 49 ] - [1 + 2 + 3..... + (x)]

Therefore,

⇒  x(x - 1) = 49 x 50 - x(x + 1)

⇒  x(x - 1) + x(x + 1) = 49 x 50

⇒ x² - x + x + x² = 49 x 50

⇒  x² = 49 x 25

Therefore, x = 7 x 5 = 35.

Since, x is not a fraction, the value of x satisfying the given condition exists and is equal to 35.

Volume of concrete required to build the first step, second step, third step, ……. (in m2) are

From the figure, it can be observed that

1st step is 1/2 m wide,

2nd step is 1 m wide,

3rd step is 3/2 m wide,

Therefore, the width of each step is increasing by 1/2 m each time whereas their height 1/4 m and length

50 m remains the same.

Therefore, the widths of these steps are

1/2,1, 3/2, 2,...

Volume of concrete in 1st step = 

Volume of concrete in 2nd step =

Volume of concrete in 3rd step =

It can be observed that the volumes of concrete in these steps are in an A.P.

 

⇒ a = 25/4

⇒ d= 25/2 - 25/4 = 25/4

and  ,

=

=

= 15/2(100) = 750

Volume of concrete required to build the terrace is 750 m³