Comparing and Ordering Fractions
What Are Fractions?
A fraction is a part of a whole.
It has two numbers:
Numerator: The top number that shows how many parts are being dealt with.
Denominator: The bottom number that shows how many equal parts the whole is divided into.
Like Fractions
Like fractions are fractions that share the same denominator.
Examples: 2/5, 3/5, 4/5.
All fractions share the same denominator (5).
Comparison of Like Fractions:
Examine the denominator: The fractions that have the same denominator represent parts of the same size.
Compare the numerators: The fraction having the highest numerator is the bigger fraction.
Example:
Compare 2/5 and 4/5
These two fractions have the same denominator, which is 5.
Compare the numerators: 2 and 4
Since 4 is greater than 2, then 4/5 is larger than 2/5.
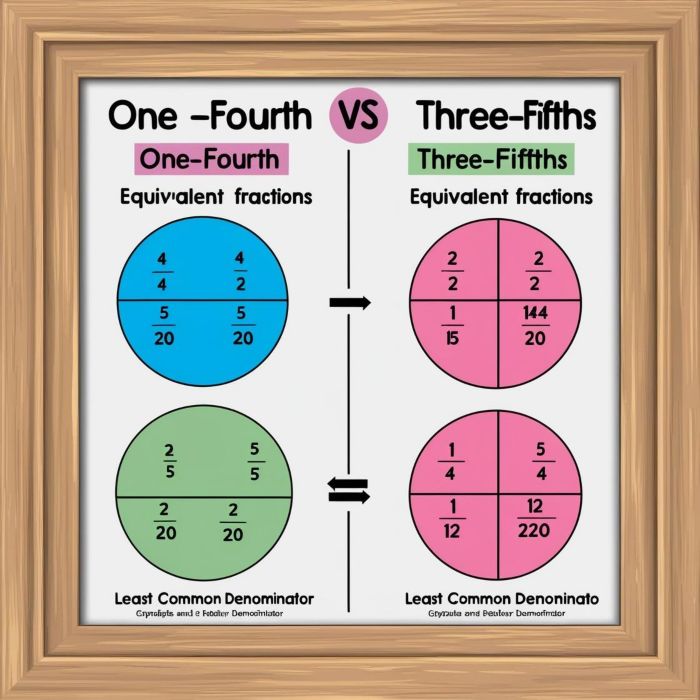
Unlike Fractions
Unlike fractions are those fractions that contain different denominators.
Example: 1/4, 3/5, 2/3.
These fractions have denominators that are different (4, 5, and 3).
Comparing Unlike Fractions:
Determine a common denominator: To compare unlike fractions, you need to determine a common denominator - the smallest number that both denominators can divide into .
Change the denominators: Write the fractions in terms of the common denominator
Compare the numerators: Once the fractions have the same denominator, compare their numerators.
Order the fractions: Put them in ascending order from the smallest to the largest, or vice versa.
How to Compare Like Fractions
-
Ensure that the denominators are equal.
-
Compare the numerators:
-
The fraction with the greater numerator is the greater fraction.
-
Compare 7/8 and 5/8:
-
Both have the same denominator (8).
-
Compare the numerators: 7 and 5.
-
7/8 is larger than 5/8.
Example:
-
Compare 1/4 and 3/5.
-
Find the LCD of 4 and 5, which is 20.
-
Rewrite 1/4 as 5/20 and 3/5 as 12/20.
-
Now compare 5/20 and 12/20.
-
Since 12 is greater than 5, then 3/5 is greater than 1/4.
-
Comparing Fractions with the Same Denominator (Like Fractions)
with Different Denominators (Unlike Fractions)
How to Compare Unlike Fractions
-
Find the least common denominator (LCD).
-
Change the fractions to equivalent fractions with the common denominator.
-
Compare the numerators:
-
The fraction with the greater numerator is the bigger fraction
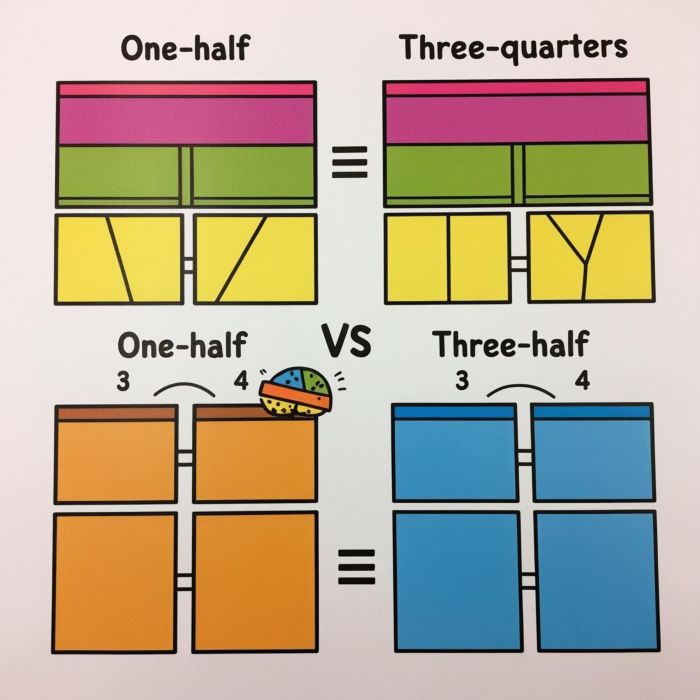
Example
-
Compare 1/2 and 3/4.
-
The LCD of 2 and 4 is 4.
-
Convert 1/2 to 2/4 and 3/4 is already in that form.
-
Compare 2/4 and 3/4.
-
3 is bigger than 2, so 3/4 is bigger than 1/2.
How To Order Like Fractions
-
Make sure the fractions have the same denominator.
-
Compare the numerators:The fraction with the smallest numerator is the smallest fraction, and the one with the largest numerator is the largest.
-
Order the fractions from smallest to largest or vice versa
Exercise:
-
Arrange 2/7, 5/7 and 3/7 from least to greatest:
-
All fractions have the same denominator (7).
-
Compare the numerators: 2, 5 and 3.
-
Least to Greatest: 2/7, 3/7, 5/7.
How to Order Unlike Fractions
-
Find a common denominator for all fractions
-
Write each fraction as an equivalent fraction using the common denominator.
-
Compare the numerators.
-
Write the fractions from least to greatest (or greatest to least).
Exercise:
-
Order these fractions from least to greatest:
-
Determine the LCD of 2, 5, and 3, which is 30.
-
Convert the fractions to have the LCD.
1/2 = 15/30
3/5 = 18/30
2/3 = 20/30
-
Now compare the fractions 15/30, 18/30, and 20/30.
-
The order from least to greatest is: 1/2, 3/5, 2/3.
Quiz
1. Which of the following is greater?
-
a) 3/8
-
b) 5/8
-
c) 2/8
-
d) 1/8
2. Which of the following is in the order from smallest to largest?
-
a) 1/2, 3/5, 2/3
-
b) 2/3, 3/5, 1/2
-
c) 1/2, 2/3, 3/5
-
d) 3/5, 2/3, 1/2
3. One of the fractions below is smaller. Which one is that?
-
a) 5/6
-
b) 4/6
-
c) 3/6
-
d) 2/6
4. Arrange the following fractions from largest to smallest: 1/4, 3/4, 2/4 .
-
a) 3/4, 2/4, 1/4
-
b) 1/4, 2/4, 3/4
-
c) 2/4, 1/4, 3/4
-
d) 1/4, 3/4, 2/4
5. Which of the following is the correct order of these unlike fractions from smallest to largest? 1/3, 2/5, 3/4
-
a) 1/3, 2/5, 3/4
-
b) 2/5, 3/4, 1/3
-
c) 3/4, 2/5, 1/3
-
d) 1/3, 3/4, 2/5
Fun Fact
1: Origin of Fractions
You know fractions have been around for thousands of years, right? Egyptian records show that the ancient Egyptians were some of the first people to use fractions! They did not use a denominator and numerator like we use today. Instead, they used unit fractions-fractions that always have a numerator of 1. So, for example, they wrote expressions like 1/2, 1/3, 1/4 and so forth. The Egyptians even wrote fractions on ancient papyrus scrolls over 4,000 years ago!
2: Fractions in Pizza
Sometimes, the most fun way to think about fractions is through using pizza! Imagine that you have a pizza cut into eight equal pieces. Then each slice of the pizza is 1/8 of the pizza. But if you eat three slices of that pizza, you have 3/8 of the pizza altogether. So every time you indulge in pizza, you're practicing your fractions! Next time you are all eating pizza with your family or friends, see how many portions of the pizza you can share
FAQs
What is the rule for ordering fractions?
To compare fractions to order them, compare their numerators when the denominators are the same, or find a common denominator for unlike fractions.
How to do comparison and ordering?
Compare fractions by finding a common denominator or by comparing the numerators if the denominators are the same.
How to teach children to compare fractions?
Instruct them to first find a common denominator and then compare the numerators or directly compare the numerators if the denominators are the same.
Which fraction is smallest?
The fraction that has the smallest numerator or the smallest equivalent value for that fraction by converting to a common denominator is the smallest.
Practice Worksheet
Easy Level Worksheets
Intermediate Level Worksheets
Advanced Level Worksheets