NCERT Solutions of Class 9 Maths Chapter 8: Quadrilaterals
"Quadrilaterals," from the NCERT Class 9 Maths syllabus, delves into the properties, types, and characteristics of quadrilaterals, a key concept in geometry. The chapter helps students understand the various angles, sides, and diagonals of quadrilaterals, and how they relate to each other.
Access Answers to NCERT Solutions of Class 9 Maths Chapter 8: Quadrilaterals
Students can access the NCERT Solutions of Class 9 Maths Chapter 8: Quadrilaterals. Curated by experts according to the CBSE syllabus for 2023–2024, these step-by-step solutions make Maths much easier to understand and learn for the students. These solutions can be used in practice by students to attain skills in solving problems, reinforce important learning objectives, and be well-prepared for tests.
Exercise 8.1
The angles of the quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Let the angles of the quadrilateral be 3x, 5x, 9x and 13x.
∴ 3x + 5x + 9x + 13x = 360°
[Angle sum property of a quadrilateral]
⇒ 30x = 360°
⇒ x =360°/30°= 12°
∴ 3x = 3 x 12° = 36°
5x = 5 x 12° = 60°
9x = 9 x 12° = 108°
13a = 13 x 12° = 156°
⇒ The required angles of the quadrilateral are 36°, 60°, 108° and 156°.
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Let ABCD is a parallelogram such that AC = BD.
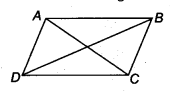
In ∆ABC and ∆DCB,
AC = DB [Given]
AB = DC [Opposite sides of a parallelogram]
BC = CB [Common]
∴ ∆ABC ≅ ∆DCB [By SSS congruency]
⇒ ∠ABC = ∠DCB [By C.P.C.T.] …(1)
Now, AB || DC and BC is a transversal. [ ∵ ABCD is a parallelogram]
∴ ∠ABC + ∠DCB = 180° … (2) [Co-interior angles]
From (1) and (2), we have
∠ABC = ∠DCB = 90°
i.e., ABCD is a parallelogram having an angle equal to 90°.
∴ ABCD is a rectangle.
Show that the diagonals of a square are equal and bisect each other at right angles.
Let ABCD be a square such that its diagonals AC and BD intersect at O.
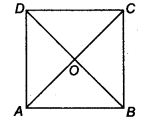
(i) To prove that the diagonals are equal, we need to prove AC = BD.
In ∆ABC and ∆BAD, we have
AB = BA [Common]
BC = AD [Sides of a square ABCD]
∠ABC = ∠BAD [Each angle is 90°]
∴ ∆ABC ≅ ∆BAD [By SAS congruency]
AC = BD [By C.P.C.T.] …(1)
(ii) AD || BC and AC is a transversal. [∵ A square is a parallelogram]
∴ ∠1 = ∠3
[Alternate interior angles are equal]
Similarly, ∠2 = ∠4
Now, in ∆OAD and ∆OCB, we have
AD = CB [Sides of a square ABCD]
∠1 = ∠3 [Proved]
∠2 = ∠4 [Proved]
∴ ∆OAD ≅ ∆OCB [By ASA congruency]
⇒ OA = OC and OD = OB [By C.P.C.T.]
i.e., the diagonals AC and BD bisect each other at O. …….(2)
(iii) In ∆OBA and ∆ODA, we have
OB = OD [Proved]
BA = DA [Sides of a square ABCD]
OA = OA [Common]
∴ ∆OBA ≅ ∆ODA [By SSS congruency]
⇒ ∠AOB = ∠AOD [By C.P.C.T.] …(3)
∵ ∠AOB and ∠AOD form a linear pair.
∴∠AOB + ∠AOD = 180°
∴∠AOB = ∠AOD = 90° [By(3)]
⇒ AC ⊥ BD …(4)
From (1), (2) and (4), we get AC and BD are equal and bisect each other at right angles.
Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.

We have a parallelogram ABCD in which diagonal AC bisects ∠A
⇒ ∠DAC = ∠BAC
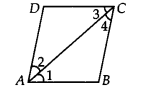
(i) Since, ABCD is a parallelogram.
∴ AB || DC and AC are transversals.
∴ ∠1 = ∠3 …(1)
[ ∵ Alternate interior angles are equal]
Also, BC || AD and AC is a transversal.
∴ ∠2 = ∠4 …(2)
[ v Alternate interior angles are equal]
Also, ∠1 = ∠2 …(3)
[ ∵ AC bisects ∠A]
From (1), (2) and (3), we have
∠3 = ∠4
⇒ AC bisects ∠C.
(ii) In ∆ABC, we have
∠1 = ∠4 [From (2) and (3)]
⇒ BC = AB …(4)
[ ∵ Sides opposite to equal angles of a ∆ are equal]
Similarly, AD = DC ……..(5)
But, ABCD is a parallelogram. [Given]
∴ AB = DC …(6)
From (4), (5) and (6), we have
AB = BC = CD = DA
Thus, ABCD is a rhombus.
ABCD is a rhombus. Show that diagonal AC bisects ∠Aas well as ∠C and diagonal BD bisects ∠B as well AS ∠D.
Since, ABCD is a rhombus.
⇒ AB = BC = CD = DA
Also, AB || CD and AD || BC
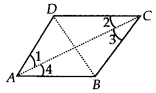
Now, CD = AD ⇒ ∠1 = ∠2 …….(1)
[ ∵ Angles opposite to equal sides of a triangle are equal]
Also, AD || BC and AC is the transversal.
[ ∵ Every rhombus is a parallelogram]
⇒ ∠1 = ∠3 …(2)
[ ∵ Alternate interior angles are equal]
From (1) and (2), we have
∠2 = ∠3 …(3)
Since, AB || DC and AC is transversal.
∴ ∠2 = ∠4 …(4)
[ ∵ Alternate interior angles are equal] From (1) and (4),
we have ∠1 = ∠4
∴ AC bisects ∠C as well as ∠A.
Similarly, we can prove that BD bisects ∠B as well as ∠D.
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that
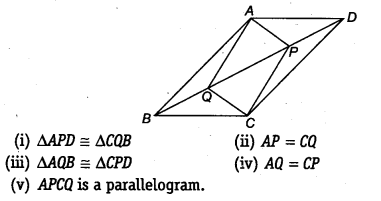
We have a parallelogram ABCD, BD is the diagonal and points P and Q are such that PD = QB
(i) Since, AD || BC and BD is a transversal.
∴ ∠ADB = ∠CBD [ ∵ Alternate interior angles are equal]
⇒ ∠ADP = ∠CBQ
Now, in ∆APD and ∆CQB, we have
AD = CB [Opposite sides of a parallelogram ABCD are equal]
PD = QB [Given]
∠ADP = ∠CBQ [Proved]
∴ ∆APD ≅ ∆CQB [By SAS congruency]
(ii) Since, ∆APD ≅ ∆CQB [Proved]
⇒ AP = CQ [By C.P.C.T.]
(iii) Since, AB || CD and BD is a transversal.
∴ ∠ABD = ∠CDB
⇒ ∠ABQ = ∠CDP
Now, in ∆AQB and ∆CPD, we have
QB = PD [Given]
∠ABQ = ∠CDP [Proved]
AB = CD [ Y Opposite sides of a parallelogram ABCD are equal]
∴ ∆AQB = ∆CPD [By SAS congruency]
(iv) Since, ∆AQB = ∆CPD [Proved]
⇒ AQ = CP [By C.P.C.T.]
(v) In a quadrilateral ∆PCQ,
Opposite sides are equal. [Proved]
∴ ∆PCQ is a parallelogram.
In ∆ABC and ∆DEF, AB = DE, AB || DE, BC – EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F, respectively (see figure).
Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
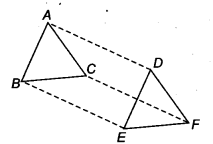
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF
(i) We have AB = DE [Given]
and AB || DE [Given]
i. e., ABED is a quadrilateral in which a pair of opposite sides (AB and DE) are parallel and of equal length.
∴ ABED is a parallelogram.
(ii) BC = EF [Given]
and BC || EF [Given]
i.e. BEFC is a quadrilateral in which a pair of opposite sides (BC and EF) are parallel and of equal length.
∴ BEFC is a parallelogram.
(iii) ABED is a parallelogram [Proved]
∴ AD || BE and AD = BE …(1)
[ ∵ Opposite sides of a parallelogram are equal and parallel] Also, BEFC is a parallelogram. [Proved]
BE || CF and BE = CF …(2)
[ ∵ Opposite sides of a parallelogram are equal and parallel]
From (1) and (2), we have
AD || CF and AD = CF
(iv) Since, AD || CF and AD = CF [Proved]
i.e., In quadrilateral ACFD, one pair of opposite sides (AD and CF) are parallel and of equal length.
∴Quadrilateral ACFD is a parallelogram.
(v) Since, ACFD is a parallelogram. [Proved]
So, AC =DF [∵ Opposite sides of a parallelogram are equal]
(vi) In ∆ABC and ∆DFF, we have
AB = DE [Given]
BC = EF [Given]
AC = DE [Proved in (v) part]
∆ABC ≅ ∆DFF [By SSS congruency]
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Let ABCD be a quadrilateral such that the diagonals AC and BD bisect each other at right angles at O.
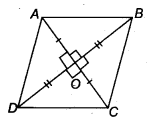
∴ In ∆AOB and ∆AOD, we have
AO = AO [Common]
OB = OD [O is the mid-point of BD]
∠AOB = ∠AOD [Each 90]
∴ ∆AQB ≅ ∆AOD [By,SAS congruency
∴ AB = AD [By C.P.C.T.] ……..(1)
Similarly, AB = BC .. .(2)
BC = CD …..(3)
CD = DA ……(4)
∴ From (1), (2), (3) and (4), we have
AB = BC = CD = DA
Thus, the quadrilateral ABCD is a rhombus.
Alternatively : ABCD can be proved first by a parallelogram then proving one pair of adjacent sides equal will result in rhombus.
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Let ABCD be a quadrilateral such that diagonals AC and BD are equal and bisect each other at right angles.
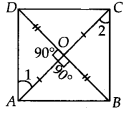
Now, in ∆AOD and ∆AOB, We have
∠AOD = ∠AOB [Each 90°]
AO = AO [Common]
OD = OB [ ∵ O is the midpoint of BD]
∴ ∆AOD ≅ ∆AOB [By SAS congruency]
⇒ AD = AB [By C.P.C.T.] …(1)
Similarly, we have
AB = BC … (2)
BC = CD …(3)
CD = DA …(4)
From (1), (2), (3) and (4), we have
AB = BC = CD = DA
∴ Quadrilateral ABCD have all sides equal.
In ∆AOD and ∆COB, we have
AO = CO [Given]
OD = OB [Given]
∠AOD = ∠COB [Vertically opposite angles]
So, ∆AOD ≅ ∆COB [By SAS congruency]
∴∠1 = ∠2 [By C.P.C.T.]
But, they form a pair of alternate interior angles.
∴ AD || BC
Similarly, AB || DC
∴ ABCD is a parallelogram.
∴ Parallelogram having all its sides equal is a rhombus.
∴ ABCD is a rhombus.
Now, in ∆ABC and ∆BAD, we have
AC = BD [Given]
BC = AD [Proved]
AB = BA [Common]
∴ ∆ABC ≅ ∆BAD [By SSS congruency]
∴ ∠ABC = ∠BAD [By C.P.C.T.] ……(5)
Since, AD || BC and AB is a transversal.
∴∠ABC + ∠BAD = 180° .. .(6) [ Co – interior angles]
⇒ ∠ABC = ∠BAD = 90° [By(5) & (6)]
So, rhombus ABCD has one angle equal to 90°.
Thus, ABCD is a square.
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal BD bisects ∠B as well as ∠D.
We have a rectangle ABCD such that AC bisects ∠A as well as ∠C.
i.e., ∠1 = ∠4 and ∠2 = ∠3 ……..(1)
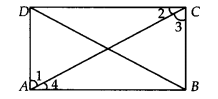
(i) Since, every rectangle is a parallelogram.
∴ ABCD is a parallelogram.
⇒ AB || CD and AC is a transversal.
∴∠2 = ∠4 …(2)
[ ∵ Alternate interior angles are equal]
From (1) and (2), we have
∠3 = ∠4
In ∆ABC, ∠3 = ∠4
⇒ AB = BC
[ ∵ Sides opposite to equal angles of a A are equal]
Similarly, CD = DA
So, ABCD is a rectangle having adjacent sides equal.
⇒ ABCD is a square.
(ii) Since, ABCD is a square and diagonals of a square bisect the opposite angles.
So, BD bisects ∠B as well as ∠D.
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see figure). Show that
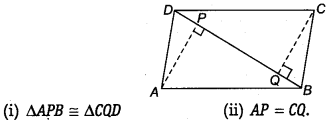
(i) In ∆APB and ∆CQD, we have
∠APB = ∠CQD [Each 90°]
AB = CD [ ∵ Opposite sides of a parallelogram ABCD are equal]
∠ABP = ∠CDQ
[ ∵ Alternate angles are equal as AB || CD and BD is a transversal]
∴ ∆APB = ∆CQD [By AAS congruency]
(ii) Since, ∆APB ≅ ∆CQD [Proved]
⇒ AP = CQ [By C.P.C.T.]
ABCD is a trapezium in which AB || CD and AD = BC (see figure). Show that
(i )∠A=∠B
(ii )∠C=∠D
(iii) ∆ABC ≅ ∆BAD
(iv) diagonal AC = diagonal BD
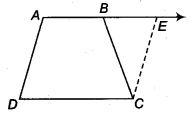
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E].
We have given a trapezium ABCD in which AB || CD and AD = BC.
(i) Produce AB to E and draw CF || AD.. .(1)
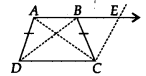
∵ AB || DC
⇒ AE || DC Also AD || CF
∴ AECD is a parallelogram.
⇒ AD = CE …(1)
[ ∵ Opposite sides of the parallelogram are equal]
But AD = BC …(2) [Given]
By (1) and (2), BC = CF
Now, in ∆BCF, we have BC = CF
⇒ ∠CEB = ∠CBE …(3)
[∵ Angles opposite to equal sides of a triangle are equal]
Also, ∠ABC + ∠CBE = 180° … (4)
[Linear pair]
and ∠A + ∠CEB = 180° …(5)
[Co-interior angles of a parallelogram ADCE]
From (4) and (5), we get
∠ABC + ∠CBE = ∠A + ∠CEB
⇒ ∠ABC = ∠A [From (3)]
⇒ ∠B = ∠A …(6)
(ii) AB || CD and AD is a transversal.
∴ ∠A + ∠D = 180° …(7) [Co-interior angles]
Similarly, ∠B + ∠C = 180° … (8)
From (7) and (8), we get
∠A + ∠D = ∠B + ∠C
⇒ ∠C = ∠D [From (6)]
(iii) In ∆ABC and ∆BAD, we have
AB = BA [Common]
BC = AD [Given]
∠ABC = ∠BAD [Proved]
∴ ∆ABC = ∆BAD [By SAS congruency]
(iv) Since, ∆ABC = ∆BAD [Proved]
⇒ AC = BD [By C.P.C.T.]
Exercise 8.2
ABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See figure). AC is a diagonal. Show that :
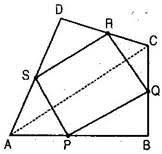
(i) SR AC and SR = 1/2AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Solution:
In ABC, P is the mid-point of AB and Q is the mid-point of BC.
Then PQ AC and PQ = 1/2 AC
(i) In ACD, R is the mid-point of CD and S is the mid-point of AD.
Then SR AC and SR = 1/2 AC
(ii) Since PQ = 1/2 AC and SR = 1/2 AC
Therefore, PQ = SR
(iii) Since PQ AC and SR
AC
Therefore, PQ SR [two lines parallel to given line are parallel to each other]
Now PQ = SR and PQ SR
Therefore, PQRS is a parallelogram.
ABCD is a rhombus and P, Q, R, S are mid-points of AB, BC, CD and DA respectively. Prove that quadrilateral PQRS is a rectangle.
Given: P, Q, R and S are the mid-points of respective sides AB, BC, CD and DA of rhombus. PQ, QR, RS and SP are joined.
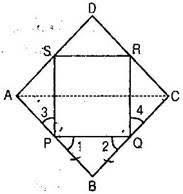
To prove: PQRS is a rectangle.
Construction: Join A and C.
Proof: In ABC, P is the mid-point of AB and Q is the mid-point of BC.
PQ
AC and PQ =
AC ……….(i)
In ADC, R is the mid-point of CD and S is the mid-point of AD.
SR
AC and SR =
AC ……….(ii)
From eq. (i) and (ii), PQ SR and PQ = SR
PQRS is a parallelogram.
Now ABCD is a rhombus. [Given]
AB = BC
AB =
BC
PB = BQ
1 =
2 [Angles opposite to equal sides are equal]
Now in triangles APS and CQR, we have,
AP = CQ [P and Q are the mid-points of AB and BC and AB = BC]
Similarly, AS = CR and PS = QR [Opposite sides of a parallelogram]
APS
CQR [By SSS congreuancy]
3 =
4 [By C.P.C.T.]
Now we have 1 +
SPQ +
3 =
And 2 +
PQR +
4 =
[Linear pairs]
1 +
SPQ +
3 =
2 +
PQR +
4
Since 1 =
2 and
3 =
4 [Proved above]
SPQ =
PQR ……….(iii)
Now PQRS is a parallelogram [Proved above]
SPQ +
PQR =
……….(iv) [Interior angles]
Using eq. (iii) and (iv),
SPQ +
SPQ =
2
SPQ =
SPQ =
Hence PQRS is a rectangle.
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rhombus.
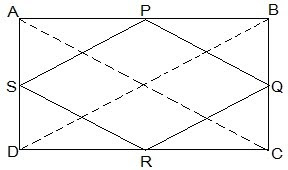
Given in the question,
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA, respectively.
Construction,
Join AC and BD.
To Prove,
PQRS is a rhombus.
Proof:
In ΔABC
P and Q are the mid-points of AB and BC, respectively
, PQ || AC and PQ = ½ AC (Midpoint theorem) — (i)
In ΔADC,
SR || AC and SR = ½ AC (Midpoint theorem) — (ii)
So, PQ || SR and PQ = SR
As in quadrilateral PQRS one pair of opposite sides is equal and parallel to each other, so, it is a parallelogram.
, PS || QR and PS = QR (Opposite sides of parallelogram) — (iii)
Now,
In ΔBCD,
Q and R are mid points of side BC and CD, respectively.
, QR || BD and QR = ½ BD (Midpoint theorem) — (iv)
AC = BD (Diagonals of a rectangle are equal) — (v)
From equations (i), (ii), (iii), (iv) and (v),
PQ = QR = SR = PS
So, PQRS is a rhombus.
Hence Proved
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
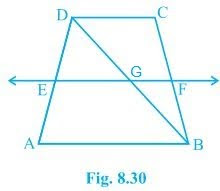
Given that,
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD.
To prove,
F is the mid-point of BC.
Proof,
BD intersected EF at G.
In ΔBAD,
E is the mid point of AD and also EG || AB.
Thus, G is the mid point of BD (Converse of mid point theorem)
Now,
In ΔBDC,
G is the mid point of BD and also GF || AB || DC.
Thus, F is the mid point of BC (Converse of mid point theorem)
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD, respectively (see Fig. 8.31). Show that the line segments AF and EC trisect the diagonal BD.
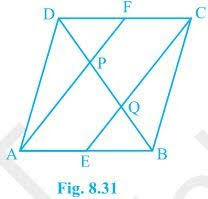
Given that,
ABCD is a parallelogram. E and F are the mid-points of sides AB and CD, respectively.
To show,
AF and EC trisect the diagonal BD.
Proof,
ABCD is a parallelogram
, AB || CD
also, AE || FC
Now,
AB = CD (Opposite sides of parallelogram ABCD)
⇒½ AB = ½ CD
⇒ AE = FC (E and F are midpoints of side AB and CD)
AECF is a parallelogram (AE and CF are parallel and equal to each other)
AF || EC (Opposite sides of a parallelogram)
Now,
In ΔDQC,
F is mid point of side DC and FP || CQ (as AF || EC).
P is the mid-point of DQ (Converse of mid-point theorem)
⇒ DP = PQ — (i)
Similarly,
In ΔAPB,
E is midpoint of side AB and EQ || AP (as AF || EC).
Q is the mid-point of PB (Converse of mid-point theorem)
⇒ PQ = QB — (ii)
From equations (i) and (i),
DP = PQ = BQ
Hence, the line segments AF and EC trisect the diagonal BD.
Hence Proved.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
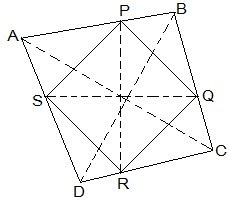
Let ABCD be a quadrilateral and P, Q, R and S the mid points of AB, BC, CD and DA, respectively.
Now,
In ΔACD,
R and S are the mid points of CD and DA, respectively.
, SR || AC.
Similarly we can show that,
PQ || AC,
PS || BD and
QR || BD
PQRS is a parallelogram.
PR and QS are the diagonals of the parallelogram PQRS. So, they will bisect each other.
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = ½ AB
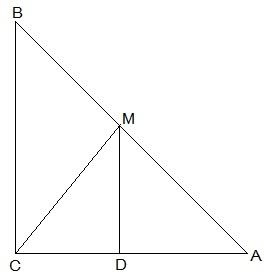
(i) In ΔACB,
M is the midpoint of AB and MD || BC
, D is the midpoint of AC (Converse of mid point theorem)
(ii) ∠ACB = ∠ADM (Corresponding angles)
also, ∠ACB = 90°
, ∠ADM = 90° and MD ⊥ AC
(iii) In ΔAMD and ΔCMD,
AD = CD (D is the midpoint of side AC)
∠ADM = ∠CDM (Each 90°)
DM = DM (common)
, ΔAMD ≅ ΔCMD [SAS congruency]
AM = CM [CPCT]
also, AM = ½ AB (M is midpoint of AB)
Hence, CM = MA = ½ AB
Frequently Asked Questions
The NCERT solution for Class 9 Chapter 8: Quadrilaterals is important as it provides a structured approach to learning, ensuring that students develop a strong understanding of foundational concepts early in their academic journey. By mastering these basics, students can build confidence and readiness for tackling more difficult concepts in their further education.
Yes, the NCERT solution for Class 9 Chapter 8: Quadrilaterals is quite useful for students in preparing for their exams. The solutions are simple, clear, and concise allowing students to understand them better. They can solve the practice questions and exercises that allow them to get exam-ready in no time.
You can get all the NCERT solutions for Class 9 Maths Chapter 8 from the official website of the Orchids International School. These solutions are tailored by subject matter experts and are very easy to understand.
Yes, students must practice all the questions provided in the NCERT solution for Class 9 Maths Chapter 8: Quadrilaterals as it will help them gain a comprehensive understanding of the concept, identify their weak areas, and strengthen their preparation.
Students can utilize the NCERT solution for Class 9 Maths Chapter 8 effectively by practicing the solutions regularly. Solve the exercises and practice questions given in the solution.

