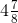(i) For subtraction of two unlike fractions, first change them to like fractions.
LCM of 1, 5 = 5
Now, let us change each of the given fractions into an equivalent fraction having 5 as the denominator.
= [(2/1) × (5/5)] = (10/5)
= [(3/5) × (1/1)] = (3/5)
Now,
= (10/5) – (3/5)
= [(10 – 3)/5]
= (7/5)
(ii) For addition of two unlike fractions, first change them to like fractions.
LCM of 1, 8 = 8
Now, let us change each of the given fractions into an equivalent fraction having 8 as the denominator.
= [(4/1) × (8/8)] = (32/8)
= [(7/8) × (1/1)] = (7/8)
Now,
= (32/8) + (7/8)
= [(32 + 7)/8]
= (39/8)
=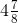
(iii) For addition of two unlike fractions, first change them to like fractions.
LCM of 5, 7 = 35
Now, let us change each of the given fractions into an equivalent fraction having 35 as the denominator.
= [(3/5) × (7/7)] = (21/35)
= [(2/7) × (5/5)] = (10/35)
Now,
= (21/35) + (10/35)
= [(21 + 10)/35]
= (31/35)
(iv) For subtraction of two unlike fractions, first change them to like fractions.
LCM of 11, 15 = 165
Now, let us change each of the given fractions into an equivalent fraction having 165 as the denominator.
= [(9/11) × (15/15)] = (135/165)
= [(4/15) × (11/11)] = (44/165)
Now,
= (135/165) – (44/165)
= [(135 – 44)/165]
= (91/165)
(v) For addition of two unlike fractions, first change them to like fractions.
LCM of 10, 5, 2 = 10
Now, let us change each of the given fractions into an equivalent fraction having 35 as the denominator.
= [(7/10) × (1/1)] = (7/10)
= [(2/5) × (2/2)] = (4/10)
= [(3/2) × (5/5)] = (15/10)
Now,
= (7/10) + (4/10) + (15/10)
= [(7 + 4 + 15)/10]
= (26/10)
= (13/5)
=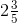
(vi) First convert mixed fraction into improper fraction,
=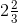 = 8/3
= 8/3
= 3 ½ = 7/2
For addition of two unlike fractions, first change them to like fractions.
LCM of 3, 2 = 6
Now, let us change each of the given fractions into an equivalent fraction having 6 as the denominator.
= [(8/3) × (2/2)] = (16/6)
= [(7/2) × (3/3)] = (21/6)
Now,
= (16/6) + (21/6)
= [(16 + 21)/6]
= (37/6)
=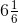
(vii) First convert mixed fraction into improper fraction,
= 8 ½ = 17/2
=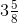 = 29/8
= 29/8
For subtraction of two unlike fractions, first change them to like fractions.
LCM of 2, 8 = 8
Now, let us change each of the given fractions into an equivalent fraction having 35 as the denominator.
= [(17/2) × (4/4)] = (68/8)
= [(29/8) × (1/1)] = (29/8)
Now,
= (68/8) – (29/8)
= [(68 – 29)/8]
= (39/8)
=