NCERT Solutions Class 11 Computer Science Chapter 2 Encoding Schemes and Number System
If you're studying Class 11 Computer Science, it would be very essential to have at least a grasp of the key concepts building the foundation. Orchids International School provides you with comprehensive NCERT solutions for Class 11 Computer Science, particularly on complex topics like Class 11 Computer Science Chapter 2: that concerns Encoding Schemes and Number Systems. The chapter makes the student understand the basics of how data is represented inside a computer. It caters to Binary, Decimal, and Hexadecimal systems with different schemes used for encoding in Computing. For detailed explanations and step-by-step solutions, one can easily download the class 11 computer science chapter 2 PDF provided by the school. Orchids International ensures students not only understand the theory behind it but also master the practical applications. The experts will help you master all the concepts so that you have a really good grasp of topics such as Encoding Schemes and Number System, setting a really good platform for further study in computer science.
Download PDF For NCERT Solutions for Computer-Science Encoding Schemes and Number System
The NCERT Solutions Class 11 Computer Science Chapter 2 Encoding Schemes and Number System are tailored to help the students master the concepts that are key to success in their classrooms. The solutions given in the PDF are developed by experts and correlate with the CBSE syllabus of 2023-2024. These solutions provide thorough explanations with a step-by-step approach to solving problems. Students can easily get a hold of the subject and learn the basics with a deeper understanding. Additionally, they can practice better, be confident, and perform well in their examinations with the support of this PDF.
Download PDF
Access Answers to NCERT Solutions Class 11 Computer Science Chapter 2 Encoding Schemes and Number System
Students can access the NCERT Solutions Class 11 Computer Science Chapter 2 Encoding Schemes and Number System. Curated by experts according to the CBSE syllabus for 2023–2024, these step-by-step solutions make Computer-Science much easier to understand and learn for the students. These solutions can be used in practice by students to attain skills in solving problems, reinforce important learning objectives, and be well-prepared for tests.
Encoding Schemes and Number System
Write base values of binary, octal and hexadecimal number systems.
|
NUMBER SYSTEM |
BASE VALUE |
|
Binary number system |
2 |
|
Octal number system |
8 |
|
hexadecimal number system |
16 |
Give full form of ASCII and ISCII.
-
The full form of ASCII is American Standard Code for Information
- The full form of ISCII is Indian Script Code for Information Interchange.
Write binary equivalent of the following octal numbers. (i) 2306 (ii) 5610 (iii) 742 (iv) 65.203
(i) 2306
|
OCTAL |
2 |
3 |
0 |
6 |
|
BINARY |
010 |
011 |
000 |
110 |
Binary Number = (10011000110)2
(ii) 5610
|
OCTAL |
5 |
6 |
1 |
0 |
|
BINARY |
101 |
110 |
001 |
000 |
Binary Number = (101110001000)2
(iii) 742
|
OCTAL |
7 |
4 |
2 |
|
BINARY |
111 |
100 |
010 |
Binary Number = (111100010)2
(iv) 65.203
|
Digits |
6 |
5 |
2 |
0 |
3 |
|
Weight |
110 |
101 |
010 |
000 |
011 |
Binary Number = (110101.010000011)2
Write binary representation of the following hexadecimal numbers. (i) 4026 (ii) BCA1 (iii) 98E (iv) 132.45
(i) 4026
|
HEXADECIMAL |
4 |
0 |
2 |
6 |
|
BINARY |
0100 |
0000 |
0010 |
0110 |
Binary Number = (100000000100110)2
(ii) BCA1
|
HEXADECIMAL |
B |
C |
A |
1 |
|
BINARY |
1011 |
1100 |
1010 |
0001 |
Binary Number = (1011110010100001)2
(iii) 98E
|
HEXADECIMAL |
9 |
8 |
E |
|
BINARY |
1001 |
1000 |
1110 |
Binary Number = (100110001110)2
(iv) 132.45
|
HEXADECIMAL |
1 |
3 |
2 |
4 |
5 |
|
BINARY |
0001 |
0011 |
0010 |
0100 |
0101 |
Binary Number = (100110010.01000101)2
The hexadecimal number system uses 16 literals (0–9, A–F). Write down its base value.
The base value of hexadecimal system is 16.
Let X be a number system having B symbols only. Write down the base value of this number system.
The base value of t number system X will be B. Because base value is the number of bits the number system contain.
What is the advantage of preparing a digital content in Indian language using UNICODE font?
UNICODE language is universally acceptable .there is no need to install any special software to recognize unlike Hindi, Marathi. UNICODE provide special value for each character. Hence, digital content in Indian language are prepared using UNICODE language.
Explore and list the steps required to type in an Indian language using UNICODE.
Step 1: write the characters, words, sentence in Indian language.
Step 2: Unicode provide unique value for each character which is readable by machine.
Step 3: system converts our Unicode to binary language/ machine language.
Try the following conversions.
(i) (514)8 = (?)10 (iv) (4D9)16 = (?)10
(ii) (220)8 = (?)2 (v) (11001010)2 = (?)10
(iii) (76F)16 = (?)10 (vi) (1010111)2 = (?)10
-
(514)8 = (?)10
|
Digits |
5 |
1 |
4 |
|
Position |
2 |
1 |
0 |
|
Weight |
82 |
81 |
80 |
Therefore,
Decimal number = 5×82 + 1×81 + 4×80
= 5×64 + 1×8 + 4× 1
= 320 + 8 + 4
= (332)10
-
(220)8 = (?)2
|
Octal Digits |
2 |
2 |
0 |
|
Binary value (3 bits) |
010 |
010 |
000 |
Therefore,
Binary number = (010010000)2
-
(76F)16 = (?)10
|
Digits |
7 |
6 |
F(15) |
|
Position |
2 |
1 |
0 |
|
Weight |
162 |
161 |
160 |
Therefore,
Decimal number = 7×162 + 6×161 + F×160
= 7×256 + 6×16 + F× 1
= 1792 + 96 + 15
= (1903)10
-
(4D9)16 = (?)10
|
Digits |
4 |
D |
9 |
|
Position |
2 |
1 |
0 |
|
Weight |
162 |
161 |
160 |
Therefore,
Decimal number = 4×162 + 13×161 + 9×160
= 4×256 + 13×16 + 9× 1
= 1024 + 208 + 9
= (1241)10
-
(11001010)2 = (?)10
|
Digits |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|
Position |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
Weight |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
Therefore,
Decimal number = 1×27+ 1×26+0×25 +0×24 +1×23 +0×22 +1×21 +0×20
= 128+64 +8 + 2
= (202)10
-
(1010111)2 = (?)10
|
Digits |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
Position |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
Weight |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
Therefore,
Decimal number = 1×26+ 0×25+1×24 +0×23 +1×22 +1×21 +1×20
= 64 +16 + 4+ 2 +1
= (87)10
Express the following octal numbers into their equivalent decimal numbers.
(i) 145
(ii) 6760
(iii) 455
(iv) 10.75
(i) 145
|
Digits |
1 |
4 |
5 |
|
Position |
2 |
1 |
0 |
|
Weight |
82 |
81 |
80 |
Therefore,
Decimal number = 1×82 +4×81 + 5×80
=1×64 + 4×8 + 5× 1
=64 + 32 + 5
= (101)10
(ii) 6760
|
Digits |
6 |
7 |
6 |
0 |
|
Position |
3 |
2 |
1 |
0 |
|
Weight |
83 |
82 |
81 |
80 |
Therefore,
Decimal number = 6×83 +7×82 +6×81 + 0×80
=6×512 + 7×64 +6×8 + 0× 1
=3072 + 448 + 48+0
= (3568)10
(i) 455
|
Digits |
4 |
5 |
5 |
|
Position |
2 |
1 |
0 |
|
Weight |
82 |
81 |
80 |
Therefore,
Decimal number = 4×82 +5×81 + 5×80
=4×64 + 5×8 + 5× 1
=256 + 40 + 5
= (301)10
(iv) 10.75
|
Digits |
1 |
0 |
7 |
5 |
|
Position |
1 |
0 |
-1 |
-2 |
|
Weight |
81 |
80 |
8-1 |
8-2 |
Therefore,
Decimal number = 1×81+0×80+7×8-1+5×8-2
=1×8+0×1+7×0.125+5×0.015625
=8+0+0.875+0.078125
= (8.953125)10
Express the following hexadecimal numbers into equivalent decimal numbers. (i) 4A2 (ii) 9E1A (iii) 6BD (iv) 6C.34
(i) 4A2
|
Digits |
4 |
A |
2 |
|
Position |
2 |
1 |
0 |
|
Weight |
162 |
161 |
160 |
Decimal number = 4 × 16 2 + A × 16 1+ 2 × 16 0
= 4 × 256 + 10 × 16 + 2 × 1
= (1186)10
(ii) 9E1A
|
Digits |
9 |
E |
1 |
A |
|
Position |
3 |
2 |
1 |
0 |
|
Weight |
163 |
162 |
161 |
160 |
Decimal number = 9 × 163 + E × 162 + 1 × 161 + A × 160
= 9 × 4096 + 14 × 256 + 1 × 16 + 10 × 1
= (40474)10
(iii) 6BD
|
Digits |
6 |
B |
D |
|
Position |
2 |
1 |
0 |
|
Weight |
162 |
161 |
160 |
Decimal number = 6 × 162 + B × 161 + D × 160
= 6 × 256 + 11 × 16 + 13 × 1
= (1725)10
(iv) 6C.34
|
Digits |
6 |
C |
3 |
4 |
|
Position |
1 |
0 |
-1 |
-2 |
|
Weight |
161 |
160 |
16-1 |
16-2 |
Decimal number = 6 × 16^1 + C × 16^0 + 3 × 16^-1 + 4 × 16^-2
= 96 + 12 × 1 + 0.1875 + 0.015625 [as C = 12 in base 16]
= (108.203125)10
How does computer understand the following text? (hint: 7 bit ASCII code). (i) HOTS (ii) Main (iii) CaSe
(i) HOTS: 072 078 084 083
|
H |
072 |
|
O |
078 |
|
T |
084 |
|
S |
83 |
(ii) Main: 077 097 105 110
|
M |
077 |
|
a |
097 |
|
i |
105 |
|
n |
110 |
(iii) CaSe: 067 097 083 101
|
C |
067 |
|
a |
097 |
|
S |
083 |
|
e |
101 |
Write the equivalent hexadecimal and binary values for each character of the phrase given below. ‘‘ हम सब एक”
|
Character |
Hexadecimal |
Binary |
|
ह |
0939 |
100100111001 |
|
म |
092E |
100100101110 |
|
स |
0938 |
100100111000 |
|
ब |
092C |
100100101100 |
|
ए |
090F |
100100001111 |
|
क |
0915 |
100100010101 |
Encode the word ‘COMPUTER’ using ASCII and convert the encode value into binary values.
|
WORD |
ASCII |
BINARY VALUE |
|
C |
067 |
01000011 |
|
O |
079 |
01001111 |
|
M |
077 |
01001101 |
|
P |
080 |
01010000 |
|
U |
085 |
01010101 |
|
T |
084 |
01010100 |
|
E |
069 |
01000101 |
|
R |
082 |
01010010 |
ASCII:
067 079 077 080 085 084 069 082
BINARY VALUE:
|
|
01000011 01001111 01001101 01010000 01010101 01010100 01000101 01010010 |
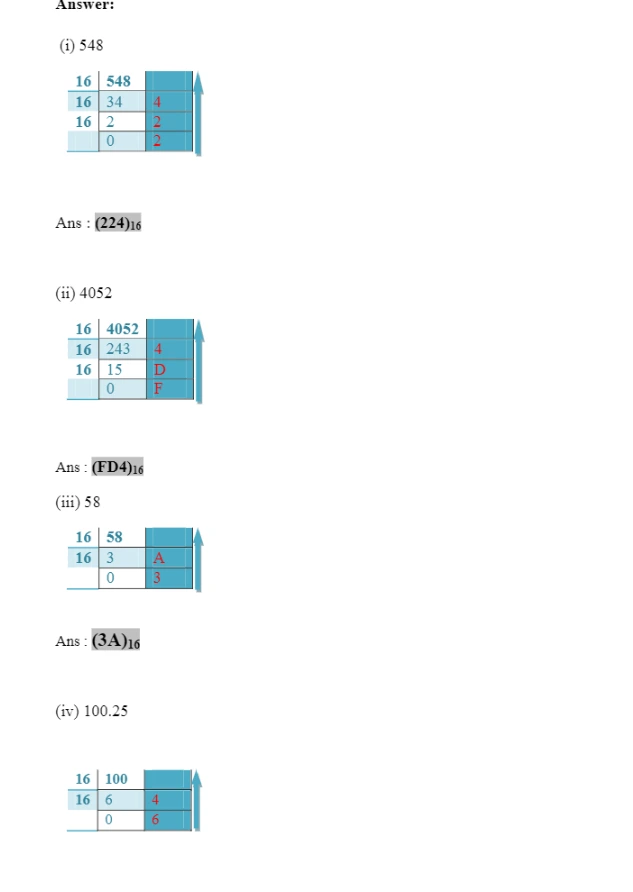
Express the following decimal numbers into hexadecimal numbers. (i) 548 (ii) 4052 (iii) 58 (iv) 100.25
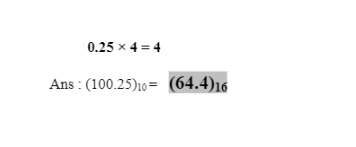
Convert the following binary numbers into octal and hexadecimal numbers. (i) 1110001000 (ii) 110110101 (iii) 1010100 (iv) 1010.1001
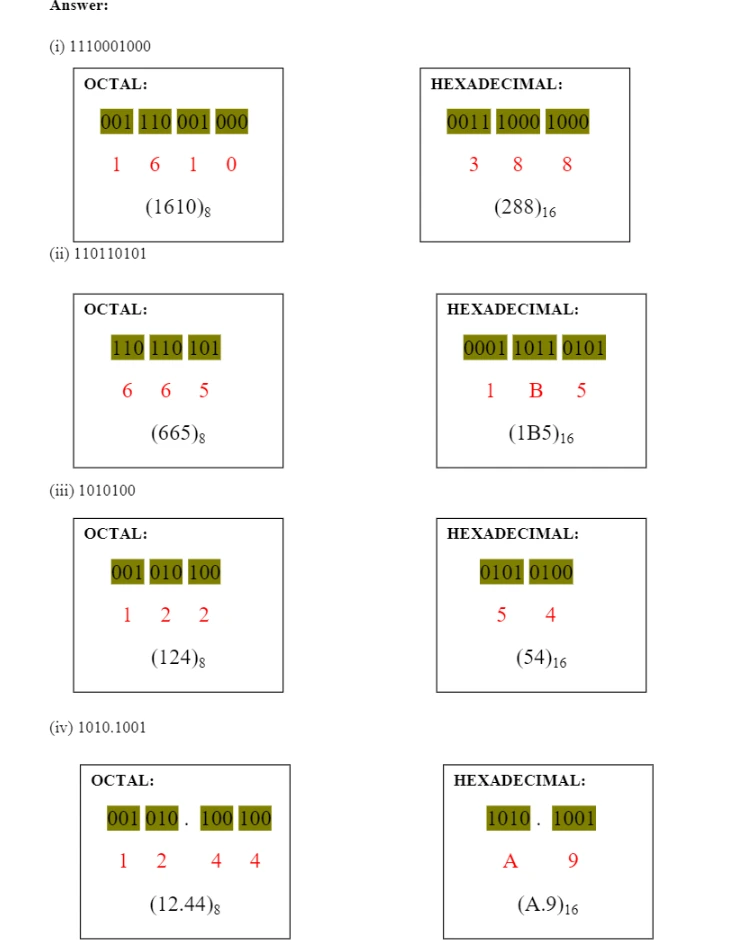
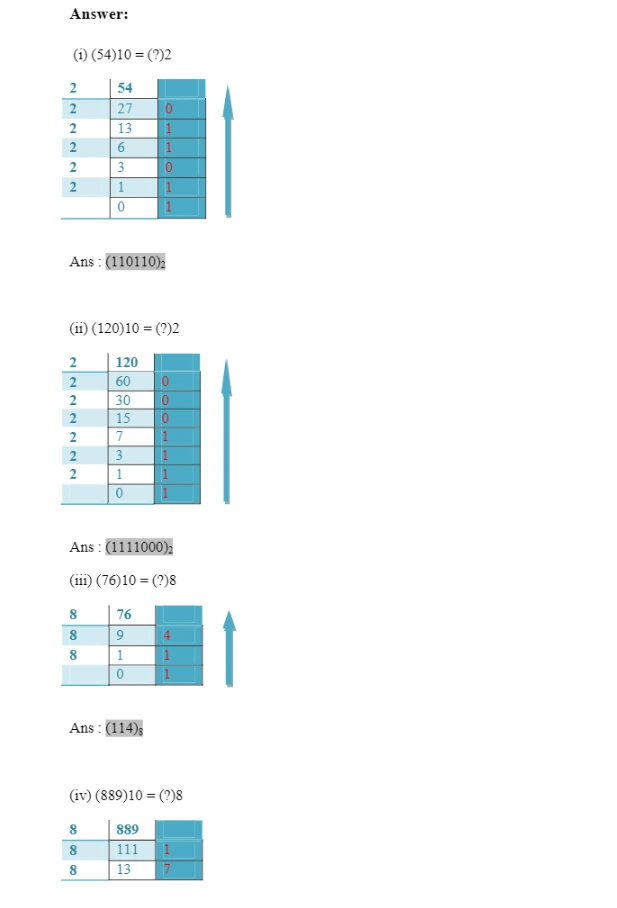
Do the following conversions from decimal number to other number systems.
(i) (54)10 = (?)2 (iv) (889)10 = (?)8
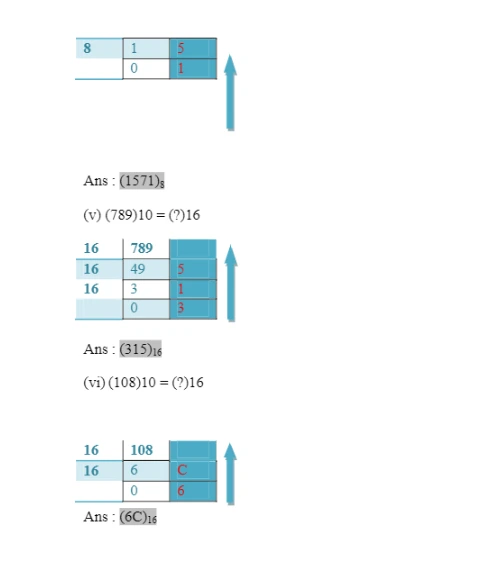
(ii) (120)10 = (?)2 (v) (789)10 = (?)16
(iii) (76)10 = (?)8 (vi) (108)10 = (?)16
Frequently Asked Questions
The NCERT solution for Class 11 Chapter 2: Encoding Schemes and Number System is important as it provides a structured approach to learning, ensuring that students develop a strong understanding of foundational concepts early in their academic journey. By mastering these basics, students can build confidence and readiness for tackling more difficult concepts in their further education.
Yes, the NCERT solution for Class 11 Chapter 2: Encoding Schemes and Number System is quite useful for students in preparing for their exams. The solutions are simple, clear, and concise allowing students to understand them better. They can solve the practice questions and exercises that allow them to get exam-ready in no time.
You can get all the NCERT solutions for Class 11 Computer Science Chapter 2 from the official website of the Orchids International School. These solutions are tailored by subject matter experts and are very easy to understand.
Yes, students must practice all the questions provided in the NCERT solution for Class 11 Computer Science Chapter 2: Encoding Schemes and Number System it will help them gain a comprehensive understanding of the concept, identify their weak areas, and strengthen their preparation.
Students can utilize the NCERT solution for Class 11 Computer Science Chapter 2 effectively by practicing the solutions regularly. Solve the exercises and practice questions given in the solution.

